Data in Wonderland

Explores communication with data in various forms through seminal and cutting-edge ideas in writing, data analyses, and visualzation.

Narrative and story can enhance others’ understanding of data, offering meaning and insights as communicated in numbers and words, or in graphical encodings. Carefully combined, narratives, data analyses, and visuals can help enable change:

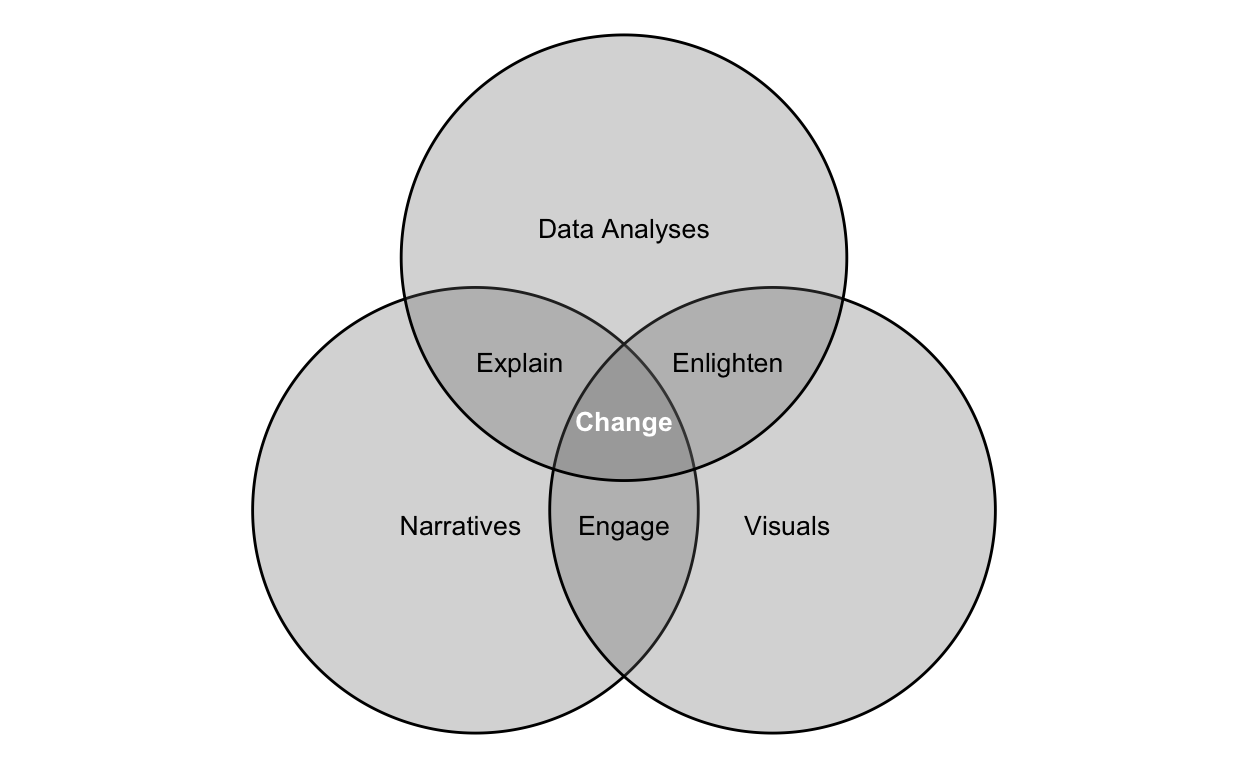
Empirical studies suggest the communication is generally more effective when its author controls all aspects of the communication, from content to typography and form. But in some cases, we may enhance the communication by allowing our audience to choose among potential contexts of the information. Here, we aim to explore many ideas within this framework, using as content a data analytics project. We will start by exploring our content (a proposed and implemented data analytics project), our intended audiences (both executives, more general, and mixed audiences), through narrative and considering not just our words but the typographic forms of those words in the chosen communication medium. Then we begin to integrate other, visual, forms of data representation into the narrative. As our discussions in graphical data encodings become more complex, we give them focus in the form of information graphics, dashboards, and finally enable our audience as, to some degree, co-author with interactive design of the communication.

The readers who will get most from this text, for whom I have in mind as my audience, are curious active learners:

An active learner asks questions, considers alternatives, questions assumptions, and even questions the trustworthiness of the author or speaker. An active learner tries to generalize specific examples, and devise specific examples for generalities.

An active learner doesn’t passively sponge up information — that doesn’t work! — but uses the readings and lecturer’s argument as a springboard for critical thought and deep understanding.

This text isn’t meant to be an end, but a beginning, giving you hand-selected, seminal and cutting-edge references for the concepts presented. Go down these rabbit holes, following citations and studying the cited material. Becoming an expert in storytelling with data also requires practicing. Indeed,

Learners need to practice, to imitate well, to be highly motivated, and to have the ability to see likenesses between dissimilar things in [domains ranging from creative writing to mathematics] (Gaut 2014).

You may find some concepts difficult or vague on a first read. For that, I’ll offer encouragement from Abelson (1995),

I have tried to make the presentation accessible and clear, but some readers may find a few sections cryptic …. Use your judgment on what to skim. If you don’t follow the occassional formulas, read the words. If you don’t understand the words, follow the music and come back to the words later.

Let’s dive in!

1 Narrative

1.1 Analytics communication scopes

1.1.1 Scopes

One place the general scope of analytics projects arise is within science (in which data science exists) and proposal writing. Let’s first just consider basic informational categories (in typical, but generic structure or order) that generally form a research proposal — see (Friedland, Folt, and Mercer 2018), (Oster and Cordo 2015), (Schimel 2012), (Oruc 2011), and (Foundation 1998), keeping in mind that the particular information and ordering explicitly depend on our intended audience:

I.  Title
II. Abstract
III. Project description
     A.  Results from prior work
     B.  Problem statement and significance
     C.  Introduction and background
         1.  Relevant literature review
         2.  Preliminary data
         3.  Conceptual, empirical, or theoretical model
         4.  Justification of approach or novel methods
     D.  Research plan
         1.  Overview of research design
         2.  Objectives or specific aims, hypotheses, and methods
         3.  Analysis and expected results
         4.  Timetable
     E.  Broader impacts
IV. References cited
V.  Budget and budget justification

While these sections are generically labelled and ordered, each should be specific to an actual proposal. Let’s consider a few sections. The title, for example, should accurately reflect the content and scope of the overall proposal. The abstract frames the goals and scope of the study, briefly describes the methods, and presents the hypotheses and expected results or outputs. It also sets up proper expectations, so be careful to avoid misleading readers into thinking that the proposal addresses anything other than the actual research topic. Try for no more than two short paragraphs.

Within the project description, the problem statement and significance typically begin with the overall scope and then funnels the reader through the hypotheses to the goals or specific aims of the research.

The literature review sets the stage for the proposal by discussing the most widely accepted or influential papers on the research. The key here is to provide context and be able to show where the proposed work would extend what has been done or how it fills a gap or resolves uncertainty, etcetera¹. We will discuss this in detail later.

Preliminary data can help establish credibility, likely success, or novelty of the proposal. But we should avoid overstating the implications of the data or suggesting we’ve already solved the problem.

In the research plan, the goal is to keep the audience focused on the overall significance, objectives, specific aims, and hypotheses while providing important methodological, technological, and analytical details. It contains the details of the implementation, analysis, and inferences of the study. Our job is typically to convince our audience that the project can be accomplished.

Objectives refer to broad, scientifically far-reaching aspects of a study, while hypotheses refer to a more specific set of testable conjectures. Specific aims focus on a particular question or hypothesis and the methods needed and outputs expected to fulfill the aims. Of note, these objectives will typically have already been (briefly) introduced earlier, for example, in the abstract. Later sections add relevant detail.

If early data are available, show how you will analyze them to reach your objectives or test your hypotheses, and discuss the scope of results you might eventually expect. If such data are unavailable, consider culling data from the literature to show how you expect the results to turn out and to show how you will analyze your data when they are available. Complete a table or diagram, or run statistical tests using the preliminary or “synthesized” data. This can be a good way to show how you would interpret the results of such data.

From studying these generic proposal categories, we get a rough sense of what we, and our audiences, may find helpful in understanding an analytics project, results, and implications: the content we communicate. Let’s now focus on analytics projects in more detail.

1.1.1.1 Data measures in analytics projects

Data analytics projects, of course, require data. What, then, are data? Let’s consider what Kelleher and Tierney (2018) has to say in their aptly titled chapter, What are data, and what is a data set? Consider their definitions:

datum : an abstraction of a real-world entity (person, object, or event). The terms variable, feature, and attribute are often used interchangeably to denote an individual abstraction.

Data are the plural of datum. And:

data set : consists of the data relating to a collection of entities, with each entity described in terms of a set of attributes. In its most basic form, a data set is organized in an \(n \cdot m\) data matrix called the analytics record, where \(n\) is the number of entities (rows) and \(m\) is the number of attributes (columns).

Data may be of different types, including nominal, ordinal, and numeric. These have sub-types as well. Nominal types are names for categories, classes, or states of things. Ordinal types are similar to nominal types, except that it is possible to rank or order categories of an ordinal type. Numeric types are measurable quantities we can represent using integer or real values. Numeric types can be measured on an interval scale or a ratio scale. The data attribute type is important as it affects our choice of analyses and visualizations.

Data can also be structured (like a table) or unstructured (more like the words in this document). And data may be in a raw form such as an original count or measurement, or it may be derived, such as an average of multiple measurements, or a functional transformation. Normally, the real value of a data analytics project is in using statistics or modelling “to derive one or more attributes that provide insight into a problem” (Kelleher and Tierney 2018).

Finally, existing data originally for one purpose may be used in an observational study, or we may conduct controlled experiments to generate data.

But it’s important to understand, on another level what data represents. Lupi (2016) offers an interesting and helpful take,

Data represents real life. It is a snapshot of the world in the same way that a picture catches a small moment in time. Numbers are always placeholders for something else, a way to capture a point of view — but sometimes this can get lost.

1.1.1.2 Understanding data requires context

Data measurements never reveal all aspects relevant to their generation or impact upon our analysis (Loukissas 2019). Loukissas (2019) provides several interesting examples where local information that generated the data matter greatly in whether we can fully understand the recorded, or measured data. His examples include plant data in an arboretum, artifact data in a museum, collection data at a library, information in the news as data, and real estate data. Using these examples, he convincingly argues we need to shift our thinking from data sets to data settings.

Let’s consider another example, from baseball. In the game, a batter that hits the pitched ball over the outfield fence between the foul poles scores for his team — he hits a home run. But a batter’s home run count in a season does not tell us the whole story of their ability to hit home runs. Let’s consider some of the context in which a home run occurs. Batters hit a home run pitched by a specific pitcher, in a specific stadium, in specific weather conditions. All of these circumstances (and more) contribute to the existence of a home run event, but that context isn’t typically considered. Sometimes partly, rarely completely.

Perhaps obviously, all pitchers have different abilities to pitch a ball in a way that affects a batter’s ability to hit the ball. Let’s leave that aside for the moment, and consider more concrete context.

In Major League Baseball there are 30 teams, each with its own stadium. But each stadium’s playing field is differently sized than the others, each stadium’s outfield fence has uneven heights, and is different from other stadium fences! To explore this context, in figure 1, hover your cursor over a particular field or fence to link them together and compare with others.

Figure 1: We cannot understand the outcome of a batter’s hit without understanding its context, including the distances and heights of each stadium’s outfield fences.

You can further explore this context in an award-winning, animated visualization (Vickars 2019, winner Kantar Information is Beautiful Awards 2019). Further, the trajectory of a hit baseball depends heavily on characteristics of the air, including density, wind speed, and direction (Adair 2017). The ball will not travel as far in cold, humid, dense air. And density depends on temperature, altitude, and humidity. Some stadiums have a roof with conditioned air protected somewhat from weather. But most are exposed. Thus, we would learn more about the qualities of a particular batter’s home run if understood in the context of these data.

Other aspects of this game are equally context-dependent. Consider each recorded ball or strike, an event made by the umpire when the batter does not swing at the ball. The umpire’s call is intended to describe location of the ball as it crosses home plate. But errors exist in that measurement. It depends on human perception, for one. We have independent measurements by a radar system (as of 2008). But that too has measurement error we can’t ignore. Firstly, there are 30 separate radar systems, one for each stadium. Secondly, those systems require periodic calibration. And calibration requires, again, human intervention. Moreover, the original radar systems installed in these stadiums in 2007 are no longer used. Different systems have been installed and used in their place. Thus, to fully understand the historical location of each pitched baseball and outcome means we must research and investigate these systems.

So when we really want to understand an event and compare among events (comparison is crucial for meaning), context matters. We’ve seen this in the baseball example, and in Loukissas’s several fascinating case study examples with many types of data. When we communicate about data, we should consider context, data settings.

1.1.1.3 Project scope

More on scope. On a high-level, it involves an iterative progression of the identification and understanding of decisions, goals and actions, methods of analysis, and data.

Figure 2: Analytic components of a general statistical workflow, adapted from Pu and Kay (2018).

The framework of identifying goals and actions, and following with information and techniques gives us a structure not unlike having the outline of a story, beginning with why we are working on a problem and ending with how we expect to solve it. Just as stories sometimes evolve when retold, our ideas and structure of the problem may shift as we progress on the project. But like the well-posed story, once we have a well-scoped project, we should be able to discuss or write about its arc — purpose, problem, analysis and solution — in relevant detail specific to our audience.

Specificity in framing and answering basic questions is important: What problem is to be solved? Is it important? Does it have impact? Do data play a role in solving the problem? Are the right data available? Is the organization ready to tackle the problem and take actions from insights? These are the initial questions of a data analytics project. Project successes inevitably depend on our specificity of answers. Be specific.

1.1.1.4 Defining goals, actions, and problems

Identifying a specific problem is the first step in any project. And a well-defined problem illuminates its importance and impact. The problem should be solvable with identified resources. If the problem seems unsolvable, try focusing on one or more aspects of the problem. Think in terms of goals, actions, data, and analysis. Our objective is to take the outcome we want to achieve and turn it into a measurable and optimizable goal.

Consider what actions can be taken to achieve the identified goal. Such actions usually need to be specific. A well-specified project ideally has a set of actions that the organization is taking — or can take — that can now be better informed through data science. While improving on existing actions is a good general starting point in defining a project, the scope does not need to be so limited. New actions may be defined too. Conversely, if the problem stated and anticipated analyses does not inform an action, it is usually not helpful in achieving organizational goals. To optimize our goal, we need to define the expected utility of each possible action.

1.1.1.5 Researching and using what is known

The general point of data analyses is to add to the conversation of what is understood. An answer, then, requires research: what’s understood? In considering how to begin, we get help from J. Harris (2017) in another context, making interesting use of texts in writing essays. We need to “situate our [data analyses] about … an issue in relation to what others have written about it.” That’s the real point of the above “literature review” that funding agencies expect, and it’s generally the place to start our work.

…

Searching for what is known involves both the “literature” on whatever issue we’re interested in, and any related data.

1.1.1.6 Identifying accessible data

Do data play a role in solving the problem? Before a project can move forward, data must be both accessible and relevant to the problem. Consider what variables each data source contributes. While some data are publicly available, other data are privately owned and permission becomes a prerequisite. And to the extent data are unavailable, we may need to setup experiments to generate it ourselves. To be sure, obtaining the right data is usually a top challenge: sometimes the variable is unmeasured or not recorded.

In cataloging the data, be specific. Identify where data are stored and in what form. Are data recorded on paper or electronically, such as in a database or on a website? Are the data structured — such as a CSV file — or unstructured, like comments on a twitter feed? Provenance is important (Moreau et al. 2008): how were the data recorded? By a human or by an instrument?

What quality are the data (Fan 2015)? Measurement error? Are observations missing? How frequently is it collected? Is it available historically, or only in real-time? Do the data have documentation describing what it represents? These are but a few questions whose answers may impact your project or approach. By extension, it affects what and how you communicate.

1.1.1.7 Identifying analyses and tools

Once data are collected, the workflow needed to bridge the gap between raw data and actions typically involves an iterative process of conducting both exploratory and confirmatory analysis (Pu and Kay 2018), see Figure 2, which employs visualization, transformation, modeling, and testing. The techniques potentially available for each of these activities may well be infinite, and each deserves a course of study in itself. Wongsuphasawat, Liu, and Heer (2019), as their title suggests, review common goals, processes, and challenges of exploratory data analysis.

Today’s tools for exploratory data analysis frequently begin by encoding data as graphics, thanks first to John Tukey, who pioneered the field in Tukey (1977), and subsequent, and applied, work in graphically exploring statistical properties of data. Cleveland (1985), the first of Cleveland’s texts on exploratory graphics, considers basic principles of graph construction (e.g., terminology, clarifying graphs, banking, scales), various graphical methods (logarithms, residuals, distributions, dot plots, grids, loess, time series, scatterplot matrices, coplots, brushing, color, statistical variation), and perception (superposed curves, color encoding, texture, reference grids, banking to 45 degrees, correlation, graphing along a common scale). His second book, Cleveland (1993), builds upon learnings of his first, and explores univariate data (quantile plots, Q-Q plots, box plots, fits and residuals, log and power transformations, etcetera), bivariate data (smooth curves, residuals, fitting, transforming factors, slicing, bivariate distributions, time series, etcetera), trivariate data (coplots, contour plots, 3-D wireframes, etcetera), hypervariate data (using scatterplot matrices and linking and brushing). Chambers (1983) in particular explores and compares distributions, explicitly considers two-dimensional data, plots in three or more dimensions, assesses distributional assumptions, and develops and assesses regression models. These three are all helpfully abstracted from any particular programming language². Unwin (2016) applies exploratory data analysis using R, examining (univariate and multivariate) continuous variables, categorical data, relationships among variables, data quality (including missingness and outliers), making comparisons, through both single graphics and an ensemble of graphics.

While these texts thoroughly discuss approaches to exploratory data analyses to help data scientists understand their own work, these do not focus on communicating analyses and results to other audiences. In this text and through references to other texts we will cover communication with other audiences.

To effectively use graphics tools for exploratory analysis requires the same understanding, if not the same approach, we need for graphically communicating with others, which we explore, beginning in section ??.

Along with visualization, we can use regression to explore data, as is well explained in the introductory textbook Gelman, Hill, and Ventari (2020), which also includes the use of graphics to explore models and estimates. These tools, and more, contribute to an overall workflow of analysis: Gelman et al. (2020) suggest best practices.

Again, the particular information and its ordering in any communication of these analyses and results depend entirely on our audience. After we begin exploring an example data analysis project, and consider workflow, we will consider audience.

1.1.2 Applying project scope: Citi Bike

Let’s develop the concept of project scope in the context of an example, one to help the bike share sponsored by Citi Bike.

You may have heard about, or even rented, a Citi Bike in New York City. Researching the history, we learn that in 2013, the New York City Department of Transportation sought to start a bike share to reduce emissions, road wear, congestion, and improve public health. After selecting an operator and sponsor, the Citi Bike bike share was established with a bike fleet distributed over a network of docking stations throughout the city. The bike share allows customers to unlock a bike at one station and return it at any other empty dock.

Might this be a problem we can find available data and conduct analyses to inform the City’s actions and further its goals?

Exercise 1 Explore the availability of bikes and docking spots as depending on users’ patterns and behaviors, events and locations at particular times, other forms of transportation, and on environmental context. What events may be correlated with or cause empty or full bike docking stations? What potential user behaviors or preferences may lead to these events? From what analogous things could we draw comparisons to provide context? How may these events and behaviors have been measured and recorded? What data are available? Where are it available? In what form? In what contexts are the data generated? In what ways may we find incomplete or missing data, or other errors in the stored measurements? May these data be sufficient to find insights through analysis, useful for decisions and goals?

Answers to questions as these provide necessary material for communication. Before digging into an analysis, let’s discuss two other aspects of workflow — reproducibility and code clarity.

1.1.3 Workflow for credible communication

Truth is tough. It will not break, like a bubble, at a touch; nay, you may kick it about all day, like a football, and it will be round and full at evening (Holmes 1894).

To be most useful, reproducible work must be credibly truthful, which means that our critics can test our language, our information, our methodologies, from start to finish. That others have not done so led to the reproducibility crisis noted in (Baker 2016):

More than 70% of researchers have tried and failed to reproduce another scientist’s experiments, and more than half have failed to reproduce their own experiments.

By reproducibility, this meta-analysis considers whether replicating a study resulted in the same statistically significant finding (some have argued that reproducibility as a measure should compare, say, a p-value across trials, not whether the p-value crossed a given threshold in each trial). Regardless, we should reproducibly build our data analyses like Holmes’s football, for our critics (later selves included) to kick it about. What does this require? Ideally, our final product should include all components of our analysis from thoughts on our goals, to identification of — and code for — collection of data, visualization, modeling, reporting and explanations of insights. In short, the critic, with the touch of her finger, should be able to reproduce our results from our work. Perhaps that sounds daunting. But with some planning and use of modern tools, reproducibility is usually practical. Guidance on assessing reproducibility and a template for reproducible workflow is described by Kitzes and co-authors (Kitzes, Turek, and Deniz 2018), along with a collection of more than 30 case studies. The authors identify three general practices that lead to reproducible work, to which I’ll add a fourth:

1. Clearly separate, label, and document all data, files, and operations that occur on data and files.

2. Document all operations fully, automating them as much as possible, and avoiding manual intervention in the workflow when feasible.

3. Design a workflow as a sequence of small steps that are glued together, with intermediate outputs from one step feeding into the next step as inputs.

4. The workflow should track your history of changes.

Several authors describe modern tools and approaches for creating a workflow that leads to reproducible research supporting credible communication, see (Gandrud 2020) and (Healy 2018a).

The workflow should include the communication. And the communication includes the code. What? Writing code to clean, transform, and analyze data may not generally be thought of as communicating. But yes! Code is language. And sometimes showing code is the most efficient way to express an idea. As such, we should strive for the most readable code possible. For our future selves. And for others. For code style advice, consult Boswell and Foucher (2011) and an update to a classic, Thomas and Hunt (2020).

1.2 Audiences and challenges

1.2.1 Audiences

Sometimes in analytics we write for ourselves, part and parcel to analysis. In another context, writer Joan Didion captured this well:

I write entirely to find out what I’m thinking, what I’m looking at, what I see, and what it means (Didion 1976).

But our introspectives are not optimal for others.

1.2.1.1 Analytics executives

Let’s imagine, for a moment, we share the mind of Citi Bike’s Chief Analytics Officer. We know what the public experiences with our bike sharing program as has, too, been reported in the news. The newspaper West Side Rag, for example, quoted Dani Simmons, our program’s spokeswoman. She explained: “Rebalancing is one of the biggest challenges of any bike share system, especially in … New York where residents don’t all work a traditional 9-5 schedule, and … people work in a variety of other neighborhoods” (Friedman 2017). As a Chief Analytics Officer, one of our jobs includes analyzing, and overseeing the analyses of, data that inform decisions for solving problems for our organization (Zetlin 2017), like rebalancing.

Would it interest us if we opened an email or memo from one of our data analysts that began:

Citi Bike, a bike sharing program, has struggled to rebalance its bikes. By rebalance, I mean taking actions that ensure customers may both rent bikes and park them at the bike sharing program’s docking stations….

Are we — Citi Bike’s Chief Analytics Officer — motivated to continue reading? Do we know why we should, or whether we should spend our time on other matters? What might we think of the data analyst from whom we received that communication?

Returning, now, to our own minds: for what audience(s), if any, might such a beginning be interesting or helpful? How can we assess whether the communication is appropriate, even optimized, and if not, adjust it to be so? That’s the focus of this text.

As we hone our skills for communicating with intended audiences, we’ll consider other minds, too: executives in analytics, marketing, chief executives, both individually and mixed with secondary or more general audiences. Consider Scott Powers, Director of Quantitative Analytics at the Los Angeles Dodgers, who earned his doctorate in statistics from Stanford University, publishes research in machine learning, codes in R, among other languages, and has worked for the Dodgers for several years.

1.2.1.2 Marketing executives

A Chief Marketing Officer shares some responsibilities with the analytics officer and other executives, while other responsibilities are primarily her own. Meet David Carr, Director of Marketing Strategy and Analysis at Digitas (a marketing agency) who has written to, and about, his marketing colleagues and their uses and misuses of data. Broadly, he or she leads responses to changing circumstances; shapes products, sales strategies, and marketing ideas, collaborating across the company.

Carr (2019) describes three main types of value that marketing drives:

1. business value: long and near-term growth, greater efficiency and enhanced productivity
2. consumer value: attitudes and behaviors that effect brand choice, frequency and loyalty
3. cultural value: shared beliefs that create a favorable environment in which to operate and influence

He illustrates his research of, and experience with, these values graphically, as a central circle, and in concentric rings identifies various characteristics and details related to these values.

Relatedly, Carr (2016) has mapped out the details for designing and managing a brand, and explained its interconnections:

The brand strategy should be influenced by the business strategy and should reflect the same strategic vision and corporate culture. In addition, the brand identity should not promise what the strategy cannot or will not deliver. There is nothing more wasteful and damaging than developing a brand identity or vision based on strategic imperative that will not get funded. An empty promise is worse than no promise.

We can tie many aspects of brand building and marketing value to measurements and data. Carr (2018) explains how marketing does — and should — work with data. His article suggests how we should craft data-driven messages for marketing executives.

1.2.1.3 Chief executives

Typically, the analytics and marketing executives report, directly or indirectly, to the CEO, who has ultimate responsibility to drive the business. Bertrand (2009) reviews empirical studies on the characteristics of CEOs. They write, while “modern-day CEOs are more likely to be generalists,” more than one quarter of those running fortune 500 companies have earned an MBA. The core educational components of the MBA program at Columbia, for example, include managerial statistics, business analytics, strategy formulation, marketing, financial accounting, corporate finance, managerial economics, global economic environment, and operations management.(Columbia University 2020) This type of curricula suggests the CEO’s vocabulary intersects with both analytics and marketing. Indeed, Bertrand explains that “current-day CEOs may require a broader set of skills as they directly interact with a larger set of employees within their organization.” If they are fluent in the basics of analytics and marketing, their responsibilities are both broader and more focused on leading the drive for creating business value. Our communications with the CEO should begin with and remained focused on how the content of our communication helps the CEO with their responsibilities.

In communicating, we should keep in mind that audiences³ have a continuum of knowledge. Everyone is a specialist on some subjects and a non-specialist on others. Moreover, even a group of all specialists could be subdivided into more specialized and less specialized readers. Specialists want details. Specialists want more detail because they can understand the technical aspects, can often use these in their own work, and require them anyway to be convinced. Non-specialists need you to bridge the gap. The less specialized your audience, the more basic information is required to bridge the gap between what they know and what the document discusses: more background at the beginning, to understand the need for and importance of the work; more interpretation at the end, to understand the relevance and implications of the findings.

Exercise 2 Identify a few analytics, marketing, and chief executives, and research their backgrounds. Describe the similarities and differences, comparing the range of skills and experience you find.

1.2.2 Challenges

1.2.2.1 Information gaps

One challenge in communicating data analytics is understanding what we see. For that, we might consider again Didion (1976)’s thoughts as part of our project. We generally revise our written words and refine our thoughts together; the improvements made in our thinking and improvements made in our writing reinforce each other (Schimel 2012). Clear writing signals clear thinking. To test our project, then, we should clarify it in writing. Once it is clear, we can begin the processes of data collection, further clarify our understanding, begin technical work, again clarify our understanding, and continuing the iterative process until we converge on interesting answers that support actions and goals.

More overlooked, to be explored here, is communicating our project effectively to others. Consider the skills typically needed for an analytics project. The qualities we need in an analytics team, writes Berinato (2018), include project management, data wrangling, data analysis, subject expertise, design, and storytelling. For that team to create value, they must first ask smart questions, wrangle the relevant data, and uncover insights. Second, the team must figure out — and communicate — what those insights mean for the business.

These communications can be challenging, however, as an interpretation gap frequently exists between data scientists and the executive decision makers they support, see (Maynard-Atem and Ludford 2020) and (Brady, Forde, and Chadwick 2017).

How can we address such a gap?

Brady and his co-authors argue that data translators should bridge the gap, address data hubris and decision-making biases, and find linguistic common ground. Subject-matter experts should be taught the quantitative skills to bridge the gap because, they continue, it is easier to teach quantitative theory than practical, business experience.

Before delving into the above arguments, let’s first consider from what perspective we’re reading. Both perspectives are written for business executives, Berinato writes in the Harvard Business Review, Brady and his co-authors write from MIT Sloan Management Review. According to HBR, their “readers have power, influence, and potential. They are senior business strategists who have achieved success and continue to strive for more. Independent thinkers who embrace new ideas. Rising stars who are aiming for the top” (“HBR Advertising and Sales,” n.d.). Similarly, MIT Sloan Management Review reports their audience: “37% of MIT SMR readers work in top management, while 72% confirm that MIT SMR generates a conversation with friends or colleagues” (“Print Advertising Opportunities” 2020). Further, all authors are in senior management. Berinato is senior editor. Brady and co-authors are consultants focusing on sports management. Why might it be important we know both an author’s background and their intended audience?

Perhaps it is not surprising for a senior executive to conclude that it would be easier to teach data science skills to a business expert than to teach the subject of a business or field to those already skilled in data science. Is this generally true? Might the background of a data translator depend upon the type of business or type of data science? Is it appropriate for this data translator to be an individual? Berinato argues that data science work requires a team. Might the responsibility of a data translator be shared?

Bridging the gap requires developing a common language. Senior management do not all use the same vocabulary and terms as analysts. Decision makers seek clear ways to receive complex insights. Plain language, aided by visuals, allow easier absorption of the meaning of data. Along with common language, data translators should foster better communication habits. Begin with questions, not assertions. Then, use analogies and anecdotes that resonate with decision makers. Finally, whomever fills this role, they must hone their skills, skills that include business and analytics knowledge, but also must learn to speak the truth, be constantly curious to learn, craft accessible questions and answers, keep high standards and attention to detail, be self-starters.

1.2.2.2 Multiple or mixed audiences

Frequently we encounter mixed audiences. Audiences are multiple, for each reader is unique. Still, readers can usefully be classified in broad categories on the basis of their proximity both to the subject matter (the content) and to the overall writing situation (the context). Primary readers are close to the situation in time and space. Uncertainty of the knowledge of a reader is like having a mixed audience, one knowing more than the other. Writing for a mixed audience is, thus, quite challenging. That challenge to write for a mixed audience is to give secondary readers information that we assume the primary readers know already while keeping the primary reader interested. The solution, conceptually, is simple: just ensure that each sentence makes an interesting statement, one that is new to all readers — even if it includes information that is new to secondary readers only. Thus, make each sentence interesting for all audiences. Let’s consider Doumont (2009d)’s examples for incorporating mixed audiences. The first sentence in his example,

We worked with IR.

may not work because IR may be unfamiliar to some in the audience. One might try to fix the issue by defining the word or, in this case, the acronym:

We worked with IR. IR stands for information Resources and is a new department.

But that isn’t ideal either because those who already know the meaning aren’t given new information. It is, in fact, pedantic. The better approach is to weave additional information, like a definition, into the information that the specialist also finds interesting, like so:

We worked with the recently launched Information Resources (IR) department.

We’ll consider these within the context of effective business writing.

1.2.3 The utility of decisions

For data analysis to grab an audience’s attention, the communication of that analysis should answer their question, “so what?” Now that the audience knows what you’ve explained, what should come of it? What does it change?

To get to such an answer we need to think about the expected utility of the information in terms of that so what. This idea, is a more formal quantification driving towards purpose for a particular audience. We’ll just introduce a few concepts without details here as this topic is advanced, given its placement in our text’s sequencing, but it’s important for future reference to have an awareness that these concepts exist.

We can combine probability distributions of expected outcomes and the utility of those outcomes to enable rational decisions (Parmigiani 2001); (Gelman et al. 2013, chap. 9). In simple terms, this means we can decide how much each possible outcome is worth and multiply that by the probability that each outcome happens. Then, we, or our audience, can choose the “optimal” one. Slightly more formally, optimal decisions choose an action that maximizes expected utility (minimizes expected loss), where the expectation is computed using a posterior distribution.

Model choice is a special case of decision-making that uses a zero-one loss function: the loss is zero when we choose the correct model, and one otherwise. Beyond model selection, a business may use as a loss function, say, for its choice of actions that maximize expected profits arising from those actions. In more general, mathematical notation, we integrate over the product of the loss function and posterior distribution,

\[\begin{equation} \min_a\left\{ \bar{L}(a) = \textrm{E}[L(a,\theta)]= \int{L(a,\theta)\cdot p(\theta \mid D)\;d\theta} \right\} \end{equation}\]

where \(a\) are actions, \(\theta\) are unobserved variables or parameters, and \(D\) are data. The seminal work by von Neumann and Morgenstern (2004) set forth the framework for rational decision-making, and J. O. Berger (1985) is a classic textbook on the intersection of statistical decision theory and Bayesian analysis. Of note, the analyses of either-or decisions, and even sequential decisions can be fairly straight-forward. Complexity grows, however, when multiple objectives or agents are involved.

Communicating our results in terms of the utility for decisions will help us bridge the gap from analysis to audience. Again, utility is an advanced topic for its placement in this text. Just have some awareness that we can inform decisions through such a process and, to the extent these details are vague, don’t worry. Move on for now.

1.3 Elements of writing

1.3.1 Purpose, audience, and craft

As we prepare to scope, and work through, a data analytics project, we must communicate variously if it is to have value. The reproducible workflow shown in the last chapter at least provides value as a communication to its immediate audience — its authors, as a reference for what they accomplished — and to those with similar needs⁴ to understand and critique the logical progression and scope of the project. That form of communication, however, will be less valuable than other communication forms for different audiences and purposes. Given the information compiled from our project — the content — we now consider communicating various aspects for other purposes and audiences.

The importance of adjusting communication is not unique to data analytics. Let’s consider, say, how communication form differs when for a news story versus an op-ed. Long-time editor of the op-ed at the New York Times explains,

The approach to argument that I learned in classes at Berkeley was much more similar to an op-ed than the inverted pyramid of daily journalism or the slow, anecdotal flow of feature stories that had dominated my professional life (Hall 2019).

The qualities of an op-ed piece must be, she writes: “surprising, concrete, and persuasive.” These qualities are similar to that we need in business communication, which generally drive decisions. All business writing begins with a) identifying the purpose for communicating and b) understanding your audiences’ scopes of knowledge and responsibilities in the problem context. Neither is trivial; both require research. To motivate this discussion, let’s consider and deconstruct two example memos — one for Citi Bike, the other for the Dodgers — written for data science projects. It will be helpful for this exercise to place both memos side-by-side for comparison as we work through them below.

1.3.1.1 Communication structure

Let’s begin discussing the communication structure from several perspectives: purpose, narrative structure, sentence structure, and effective redundancy through hierarchy. Then, we consider audiences, story, and the importance of revision.

1.3.1.1.1 Purpose and audience

In the first example, we return to Citi Bike. After project ideation, and scoping, we want to ask Citi Bike’s head of data analytics to let us write a more detailed proposal to conduct the data analytics project. We accomplish this in 250 words. The the fully composed, draft memo follow,

Example 1 (250-word Citi Bike memo)
Michael Frumin
Director of Product and Data Science
for Transit, Bikes, and Scooters at Lyft

To inform the public on rebalancing, let’s re-explore docking
availability and bike usage, this time with subway and weather.

Let’s re-explore station and ride data in the context of subway and weather information to gain insight for “rebalancing,” what our Dani Simmons explains is ”one of the biggest challenges of any bike share system, especially in … New York where residents don’t all work a traditional 9-5 schedule, and though there is a Central Business District, it’s a huge one and people work in a variety of other neighborhoods as well” (Friedman 2017).

Recalling the previous, public study by Columbia University Center for Spatial Research (Saldarriaga 2013), it identified trends in bike usage using heatmaps. As those visualizations did not combine dimensions of space and time, which the public would find helpful to see trends in bike and station availability by neighborhood throughout a day, we can begin our analysis there.

We’ll use published data from NYC OpenData and The Open Bus Project, including date, time, station ID, and ride instances for all our docking stations and bikes since we began service. To begin, we can visually explore the intersection of trends in both time and location with this data to understand problematic neighborhoods and, even, individual stations, using current data.

Then, we will build upon the initial work, exploring causal factors such as the availability of alternative transportation (e.g., subway stations near docking stations) and weather. Both of which, we have available data that can be joined using timestamps.

The project aligns with our goals and shows the public that we are, in Simmons’s words, “innovative in how we meet this challenge.” Let’s draft a detailed proposal.

Sincerely,
Scott Spencer

---

Friedman, Matthew. “Citi Bike Racks Continue to Go Empty Just When Upper West Siders Need Them.” News. West Side Rag (blog), August 19, 2017. https://www.westsiderag.com/2017/08/19/citi-bike-racks-continue-to-go-empty-just-when-upper-west-siders-need-them.

Saldarriaga, Juan Francisco. “CitiBike Rebalancing Study.” Spatial Information Design Lab, Columbia University, 2013. https://c4sr.columbia.edu/projects/citibike-rebalancing-study.

It begins, in the title of this memo, with our purpose of writing, to conduct data analysis on specifically identified data to inform the issue of rebalancing, one of Citi Bike’s goals:

To inform rebalancing, let’s explore docking and bike availability in the context of subway and weather information.

This is what Doumont (2009d) calls a message. We should craft communications with messages, not merely information. Doumont explains that a message differs from raw information in that it presents “intelligent added value,” that is, something to understand about the information. A message interprets the information for a specific audience and for a specific purpose. It conveys the so what, whereas information merely conveys the what. What makes our title a message? Before answering this, let’s compare one of Doumont’s examples of information to that of a message. This sentence is mere information:

A concentration of 175 \(\mu g\) per \(m^3\) has been observed in urban areas.

A message, in contrast to information, would be the so what:

The concentration in urban areas (175 \(\mu g / m^3\)) is unacceptably high.

In our title, we request an action, approval for the exploratory analysis on specified data, for a particular purpose, to inform rebalancing. This purpose also implies the so what: unavailable bikes or docking slots, unbalanced stations, are bad. We’re asking to help remedy the issue.

This beginning, if effective, is only because we wrote it for a particular audience. Our audience is head of data analytics at Citi Bike, and presumably knows the problem of rebalancing; it is well-known in, and beyond, the organization. Thus, our sentence implicitly refers back to information our audience already knows⁵. Relying on his or her knowledge means we do not need to first explain what rebalancing is or why it is a problem.

Let’s introduce a second example before digging further into the structure of the Citi Bike memo. Having multiple examples to analyze has the added benefit of allowing us to induce some general, but effective, writing principles.

Considering a second example, professional teams in the sport of baseball, including the Los Angeles Dodgers, make strategic decisions within the boundaries of the sport’s rules for the purpose of winning games. One of those rules involves stealing bases, as in figure 3.

Figure 3: In a close call, the baseball umpire spread his arms, signaling that the Dodgers baserunner successfully ran to the base faster than the catcher could throw the ball to the base to get him out — the runner stole the base. Knowing when to try to steal is strategic and depends on other events that are at least partly measured as data.

This concept is part of our next example, written to the Los Angeles Dodgers’s Director of Quantitative Analytics, Scott Powers. Powers, is Director of Quantitative Analytics at the Los Angeles Dodgers. He earned his doctor of philosophy in statistics from Stanford, has authored publications in machine learning, knows R programming, and as an employee of the Dodgers, knows their history. Powers manages a team of data scientists; their responsibilities include assessing player and team performance. The draft memo follows,

Example 2 (250-word Dodgers memo)
Scott Powers
Director of quantitative analysis
at Los Angeles Dodgers

Our game decisions should optimize expectations.
Let’s test the concept by modeling decisions to steal.

Our Sandy Koufax pitched a perfect game, the most likely event sequence, only once: those, we do not expect or plan. Since our decisions based on other most likely events don’t align with expected outcomes, we leave wins unclaimed. To claim them, let’s base decisions on expectations flowing from decision theory and probability models. A joint model of all events works best, but we can start small with, say, decisions to steal second base.

After defining our objective (e.g. optimize expected runs) we will, from Statcast data, weight everything that could happen by its probability and accumulate these probability distributions. Joint distributions of all events, an eventual goal, will allow us to ask counterfactuals — “what if we do this” or “what if our opponent does that” — and simulate games to learn how decisions change win probability. It enables optimal strategy.

Rational and optimal, this approach is more efficient for gaining wins. For perspective, each added win from the free-agent market costs 10 million, give or take, and the league salary cap prevents unlimited spend on talent. There is no cap, however, on investing in rational decision processes.

Computational issues are being addressed in Stan, a tool that enables inferences through advanced simulations. This open-source software is free but teaching its applications will require time. To shorten our learning curve, we can start with Stan interfaces that use familiar syntax (like lme4) but return joint probability distributions: R packages rethinking, brms, or rstanarm. Perfect games aside, we can test the concept with decisions to steal.

Sincerely,
Scott Spencer

The beginning of this memo reads:

Our game decisions should optimize expectations. Let’s test the concept by modeling decisions to steal.

In the first three words, the subject of this sentence, signals to our audience something they have experience with: our game decisions. It’s familiar. Then, we provide a call to action: our game decisions should optimize expectations. Let’s test the concept by modeling decisions to steal. As with the Citi Bike memo (example 1), the Dodgers memo (example 2) begins with a message and stated purpose. And as with Citi Bike, the information in the title message of the Dodgers memo is shared knowledge with our audience. In fact, we rely on the educational background of our audience, who we know has earned a doctor of philosophy in statistics, when including the concept to “optimize expectations”⁶ without first explaining what that is because we know, or from the audience’s background, can assume the audience understands the concept.

So in both cases, we have begun with language and topics already familiar to the audience, which follows the more general writing advice from Doumont (2009d) , who instructs us to

put ourselves in the shoes of the audience, anticipating their situation, their needs, their expectations. Structure the story along their line of reasoning, recognizing the constraints they might bring: their familiarity with the topic, their mastery of the language, the time they can free for us.

What else do we know about chief analytics officers in general? Their jobs require them to be efficient with their time. Thus, by starting with our purpose, letting them know what we want them to do, we are considerate of their “constraints” and “time they can free for us.”

Beginning with a purpose and call-to-action also allow the executive to understand the memo’s relevance to them, in terms of their decision-making, immediately; they have a reason to continue reading.

The persuasive power of beginning with the main message for your audience, or issue relevant to your audience, is nearly as timeless as it is true. Cicero, the Roman philosopher with a treatise on rhetoric, explained that we must not begin with details because “it forms no part of the question, and men are at first desirous to learn the very point that is to come under their judgment” (Cicero and Watson 1986).

Next, let’s review the structure of these memos to see whether we’ve “structur[ed] the story along their line of reasoning.”

1.3.1.1.2 Common ground

Let’s compare the first sentences of the body of both examples. The Citi Bike memo begins,

Let’s re-explore station and ride data in the context of subway and weather information to gain insight for “rebalancing,” broadening the factors we’ve told the public that “one of the biggest challenges of any bike share system, especially in … New York where residents don’t all work a traditional 9-5 schedule, and though there is a Central Business District, it’s a huge one and people work in a variety of other neighborhoods as well” (Friedman 2017).

This sentence starts with the title request, and then ties the purpose — rebalancing — to corporate goals. It does so by quoting the company’s spokesperson, which serves as both evidence of the so what. Offering, and accepting, Simmons’s quote serves a second purpose in writing: it helps to establish common ground with our audience.

If we want to affect the behaviors and beliefs of the person in front of us, we need to first understand what goes on inside their head and establish common ground. Why? When you provide someone with new data, they quickly accept evidence that confirms their preconceived notions (what are known as prior beliefs) and assess counter evidence with a critical eye (Sharot 2017). Four factors come into play when people form a new belief: our old belief (this is technically known as the “prior”), our confidence in that old belief, the new evidence, and our confidence in that evidence. Focusing on what you and your audience have in common, rather than what you disagree about, enables change. Let’s check for common ground in the Dodgers memo. The first sentence of the body begins,

Our Sandy Koufax pitched a perfect game, the most likely event sequence, only once: those, we do not expect or plan.

Sandy Koufax is one of the most successful Dodgers players in the history of the franchise. He is one of less than 20 pitchers in the history of baseball to pitch a perfect game, something extraordinary. Our audience, as an employee of the Dodgers, will be familiar with this history. It is also something very positive — and shared — between author and audience. It is intended to establish common ground, in two ways. Along with that positive, shared history, it sets up an example of a statistical mode, one that we know the audience would agree is unhelpful for planning game strategy because it is too rare, even if it is a statistical mode. It helps to create common ground or agreement that it may not be best to use statistical modes for making decisions.

In both memos, we are also trying to use an interesting fact that may be unexpected or surprising in this context (Sandy Koufax, Dani Simmons) to grab our audience’s attention. In journalism, this is one way to create the lead. Zinsser (2001)⁷ explains that the most important sentence in any communication is the first one. If it doesn’t induce the reader to proceed to the second sentence, your communication is dead. And if the second sentence doesn’t induce the audience to continue to the third sentence, it’s equally dead. Readers want to know — very soon — what’s in it for them.

Your lead must capture the audience immediately cajoling them with freshness, or novelty, or paradox, or humor, or surprise, or with an unusual idea, or an interesting fact, or a question. Next, it must provide hard details that tell the audience why the piece was written and why they ought to read it.

1.3.1.1.3 Details

At this point in both memos, we have begun our memo with information familiar to our audience, relevant to their job in decision-making, and established our purpose. We have also started with information they would agree with. We’ve created common ground. The stage is set. What’s next? Here’s the next two sentences in the body of the Citi Bike memo:

Recalling the previous, public study by Columbia University Center for Spatial Research (Saldarriaga 2013), it identified trends in bike usage using heatmaps. As those visualizations did not combine dimensions of space and time, which the public would find helpful to see trends in bike and station availability by neighborhood throughout a day, we can begin our analysis there.

The first sentence introduces previous work — background — on rebalancing studies and its limitations, and we proposed to start where the prior work stopped. This accomplishes two objectives. First, it helps our audience understand beginning details of our proposed project. Second, it helps the audience see that our proposed work is not redundant to what we already know. Thus, we began the details of our proposed solution. What is described in the Dodgers memo at a similar point? This:

To claim them, let’s base decisions on expectations flowing from decision theory and probability models. A joint model of all events works best, but we can start small with, say, decisions to steal second base.

As with Citi Bike, the next two sentences start introducing details of the proposed project.

After introducing the nature of the proposed project in both memos, we identify data that makes the proposed project feasible. In the Citi Bike memo we identify specific categories of data and the publicly available source of those data:

We’ll use published data from NYC OpenData and The Open Bus Project, including date, time, station ID, and ride instances for all our docking stations and bikes since we began service.

Similarly, in the Dodgers memo,

After defining our objective (e.g. optimize expected runs) we will, from Statcast data, weight everything that could happen by its probability and accumulate these probability distributions.

It may seem we are less descriptive of the data than in the Citi Bike memo, but the label “Statcast” signals to our particular audience a group of specific, publicly available variables collected by the Statcast system, see (Willman, n.d.) and (Willman 2020).

After identifying data, we explain how we plan its analysis.

Having identified data, both memos then describe more details of our proposed methodology. In Citi Bike, we discuss two stages. We plan to graphically explore specific variables in search of specific trends first.

To begin, we can visually explore the intersection of trends in both time and location with this data to understand problematic neighborhoods and, even, individual stations, using current data.

Then, we specifically identify additional data we plan to join and explore as causal factors for problem areas:

Then, we will build upon the initial work, exploring causal factors such as the availability of alternative transportation (e.g., subway stations near docking stations) and weather. Both of which, we have available data that can be joined using timestamps.

Similarly, in the Dodgers memo, go into the planned methodology. We plan to model expectations from the data:

…from Statcast data, weight everything that could happen by its probability and accumulate these probability distributions.

1.3.1.1.4 Benefits

Having described our data and methodology in both memos, we now describe some benefits. In the Citi Bike memo,

The project aligns with our goals and shows the public that we are, in Simmons’s words, “innovative in how we meet this challenge.”

And in the Dodgers memo, perhaps because we believe the benefits are comparatively less obvious, or less proven, we further develop them:

Joint distributions of all events, an eventual goal, will allow us to ask counterfactuals — “what if we do this” or “what if our opponent does that” — and simulate games to learn how decisions change win probability. It enables optimal strategy.

Rational and optimal, this approach is more efficient for gaining wins. For perspective, each added win from the free-agent market costs 10 million, give or take, and the league salary cap prevents unlimited spend on talent. There is no cap, however, on investing in rational decision processes.

1.3.1.1.5 Limitations

In the Citi Bike memo, we didn’t identify limitations. Should we?

In the Dodgers memo, we do, while also explaining how we plan to overcome those limitations:

Computational issues are being addressed in Stan, a tool that enables inferences through advanced simulations. This open-source software is free but teaching its applications will require time. To shorten our learning curve, we can start with Stan interfaces that use familiar syntax (like lme4) but return joint probability distributions: R packages rethinking, brms, or rstanarm.

1.3.1.1.6 Conclusion

Finally, we wrap up in both memos. in the Citi Bike memo, after echoing the quote from Simmons, we state,

Let’s draft a detailed proposal.

Again, the Dodgers memo is similar. There, we circle back to our introduction to Sandy Koufax and his perfect game, then conclude,

Perfect games aside, we can test the concept with decisions to steal.

Again, this idea of echoing something from where we began is journalism’s complement to the lead.

Zinsser explains that, ideally, the ending should encapsulate the idea of the piece and conclude with a sentence that jolts us with its fitness or unexpectedness. Consider bringing the story full circle — to strike at the end an echo of a note that was sounded at the beginning. It gratifies a sense of symmetry.

Executives’ lines of reasoning commonly, but do not always, follow the general document structure described above. If we don’t have information otherwise, this is a good start.

1.3.1.2 Narrative structure

The above ideas — tools — are helpful in structuring and writing persuasive memos, and longer communications for that matter. And as writing lengthens, the next couple of related tools can be especially helpful in refining the narrative structure in a way that holds our audience’s interest by creating tension. German dramatist Gustav Freytag in the late 19th century illustrated a narrative arc⁸ used in Shakespearean dramas:

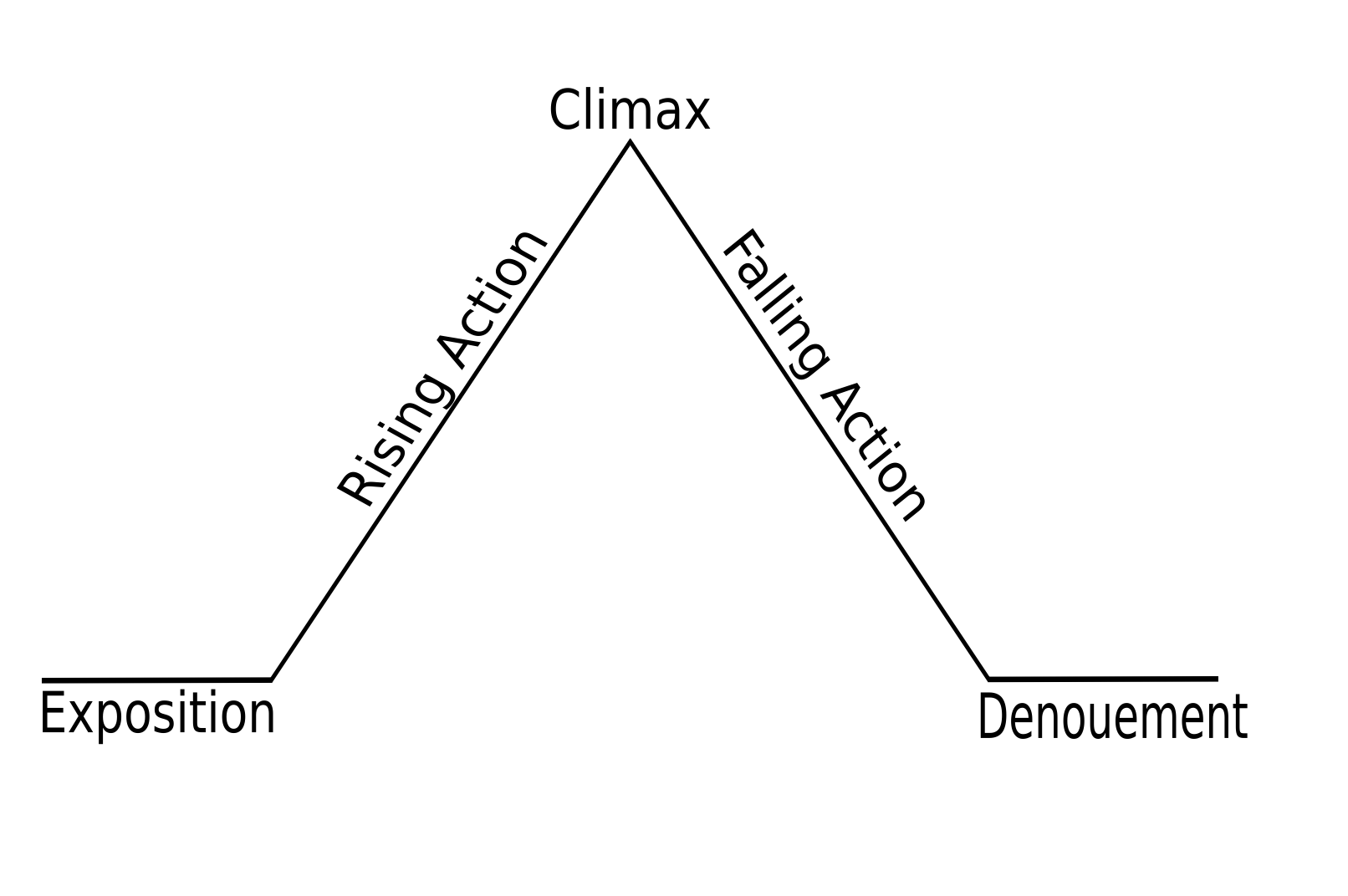
The primary elements of an applied analytics project may be thought of as a well-articulated business problem, a data science solution, and a measurable outcome to produce value for the organization. The analytics project may thus be conceptualized as a narrative arc, with a beginning (problem), middle (analytics), and end (overcoming of the problem), along with characters (analysts, colleagues, clients) who play important roles.

Duarte (2010) used the narrative arc to conceptualize an interesting alternative way to think about structure that creates tension: alternating what is with what may be:

We can repeat this approach, see figure 4, switching between what is and what may be to maintain a sense of tension or interest throughout a narrative arc. Once you become aware, you may be surprised how much you find writing in this form.

Figure 4: Duarte illustrates the repeated switching between what is and what may be, which helps to hold audience interest throughout a narrative.

This juxtaposition of two states for creating tension is another form of comparison.

Exercise 3 Revisit the two memos, examples 1 and 2. Identify sentences or paired sentences that shift focus from what is to what could be, creating a contrast.

Let’s look closer, now, to sentence structure.

1.3.1.3 Sentence structure

When we describe old before new, using sentence structure, it generally improves understanding. The concept has also been described as an information unit. “The information unit is what its name implies: a unit of information. Information, in this technical grammatical sense, is the tension between what is already known or predictable and what is new or unpredictable” (Halliday and Matthiessen 2004). As a general principle, “readers follow a story most easily if they can begin each sentence with a character or idea that is familiar to them, either because it was already mentioned or because it comes from the context” (J. M. Williams, Bizup, and Fitzgerald 2016).

Consider an alternative flow of information. Put new information before old information. Reversing the information flow will likely confuse your audience. This point was clearly demonstrated in a classic movie, Memento,

Figure 5: Poster for Memento, a movie designed to purposefully confuse the audience by narrating the story (partly) in reverse.

where Director Christopher Nolan tells the story of a man with anterograde amnesia (the inability to form new memories) searching for someone who attacked him and killed his wife, using an intricate system of Polaroid photographs and tattoos to track information he cannot remember. The story is presented as two different sequences of scenes interspersed during the film: a series in black-and-white that is shown chronologically, and a series of color sequences shown in reverse order (simulating for the audience the mental state of the protagonist). The two sequences meet at the end of the film, producing one complete and cohesive narrative. Yet, the reversed order is (effectively) designed to hold the audience in confusion so that they may get a sense of the confusion experienced by someone with this illness. Indeed, that we demonstrate this with film implies that ordering in visual representation matters too, and it does. As such, we revisit this in the context of images.

For reasons similar, explain complex information last. This is particularly important in three contexts: introducing a new technical term, presenting a long or complex unit of information, introducing a concept before developing its details. And just as the old—new paradigm helps to convey messages, so too does expressing crucial actions in verbs. Make your central characters the subjects of those verbs; keep those subjects short, concrete, and specific.

Exercise 4 Revisit the Dodgers memo again, example 2. This time, for each sentence and words within the sentence, try to identify whether the word or phrase is new or old. When determining this, consider both the words, phrases, and sentences preceding the one under analysis. Of note, you may also consider the audience’s background knowledge as a form of information.

1.3.1.4 Layering and heirarchy

Most communications benefit by providing multiple levels in which the narrative may be read. Even emails and memos — concise communications — enable two layers, the title and the main body. Thus, the title should inform the audience of the relevance of the communication: what is it the author wants them to do or know. It should also, or at least, invite the audience to learn more through the details of the main body. As the communication lengthens, more layers may be used. The title’s purpose remains the same, as does the main body. But we may add middle layers, headers and subheaders (Doumont 2009d). These should not be generic. Instead, the author should be able to read just these and understand the gist of the communication. This concept is well established where we intend persuasive communication. A well-known instructor of legal writing, Guberman (2014) explains how to draft this middle layer:

Strong headings are like a good headline for a newspaper article: they give [the audience] the gist of what [they] need to know, draw [them] into text [they] might otherwise skip, and even allow … a splash of creativity and flair.

The old test is still the best. Could [the audience] skim your headings and subheadings and know why [they should act]?

A good way to provide these “signposts” is to make your headings complete thoughts that, if true, would push you toward the finish line.

In accord, Scalia and Garner (2008) writes:

Since clarity is the all-important objective, it helps to let the reader know in advance what topic you’re to discuss. Headings are most effective if they’re full sentences announcing not just the topic but your position on that topic.

In short, headings should be what Doumont (2009d) calls messages. Headings provide “effective redundancy.” The redundancy gained from headers may be two fold. They, first, introduce your message before the detailed paragraphs and, second, may be collected up front, as a table of contents. Even short communication benefit from headers, and communications of at least several pages will likely benefit from such a table of contents along with headers.

1.3.1.5 Story

At this point, we’ve identified a problem or opportunity upon which our entity may decide to act. We’ve found data and considered how we might uncover insights to inform decisions. We’ve scoped an analytics project. In beginning to write, we’ve considered document structure, sentence structure, and narrative. We’ve also begun to consider our audience.

Can we — should we — use story to help us communicate? Consider its use in the context of an academic debate on the question: (Krzywinski and Cairo 2013a), (Katz 2013), and (Krzywinski and Cairo 2013b); and for more perspective: (Gelman and Basbøll 2014).

Exercise 5 Explain whether, and why or why not, you believe any of the arguments in the debate about using story to explain scientific results are correct.

Let’s now focus on how we may directly employ story. A little research on story, though, reveals differences in use of the term. “"Story, n."” (2015) defines story generally as a narrative:

An oral or written narrative account of events that occurred or are believed to have occurred in the past…

Distinguished novelist E.M. Forster famously described story as “a series of events arranged in their time sequence.” Of note, he also compares and distinguishes story from plot: “plot is also a narrative of events, the emphasis falling on causality: ‘The king died and then the queen died’ is a story. But ‘the king died and then the queen died of grief’ is a plot. The time sequence is preserved, but the sense of causality overshadows it” (Forster 1927). But not just any narrative works for moving our audiences to act. Harari (2014) explains,

the difficulty lies not in telling the story, but in convincing everyone else to believe it. . .

Let’s consider other points of view.

To understand the narrative arc of successful stories, John Yorke studied numerous stories, and from those induced general principles Yorke (2015). A journalist and author, too, has studied narrative structure but, with a different approach — he focuses on the cognitive science and psychology of how our mind works and relates those characteristics to story (Storr 2020). Story, writes Storr, typically begins with “unexpected change”, the “opening of an an information gap”, or both. Humans naturally want to understand the change, or close that gap; it becomes their goal. Language of messages and information that close the gap, then, form what we may think of as narrative’s plot.

Indeed, Storr (2020) suggests that the varying so-called designs for plot structure⁹ are all really different approaches to describing change:

But I suspect that none of these plot designs is actually the ‘right’ one. Beyond the basic three acts of Western storytelling, the only plot fundamental is that there must be regular change, much of which should preferably be driven by the protagonist, who changes along with it. It’s change that obsesses brains. The challenge that storytellers face is creating a plot that has enough unexpected change to hold attention over the course of an entire novel or film. This isn’t easy. For me, these different plot designs represent different methods of solving that complex problem. Each one is a unique recipe for a plot that moves relentlessly forwards, builds in intrigue and tension and never stops changing.

A quantitative analysis of over 100,000 narratives suggests this too (Robinson 2017).

We evolved for recognizing change, and for cause and effect. Thus, a narrative or story is driven forward by linking together change after change as instances of cause and effect. Indeed, to create initial interest, we only need to foreshadow change.

Let’s consider some examples that use information gaps and narratives in the context of data science. The short narratives in Wainer (2016b), each about a data science concept that people frequently misunderstand, are exemplary. He begins each of these by setting up a contrast or information gap. In chapter 1, for example, the author teaches the “Rule of 72” as a heuristic to think about compounding quantities by posing a question¹⁰ to setup an information gap:

Great news! You have won a lottery and you can choose between one of two prizes. You can opt for either:

1. $10,000 every day for a month, or

2. One penny on the first day of the month, two on the second, four on the third, and continued doubling every day thereafter for the entire month.

Which option would you prefer?

Similarly, in chapter 2, Wainer (2016b) teaches us implications of the law of large numbers by exposing an information gap. Again, he uses a question to setup an information gap:

“Virtuosos becoming a dime a dozen,” exclaimed Anthony Tommasini, chief music critic of the New York Times in his column in the arts section of that newspaper on Sunday, August 14, 2011.

…

But why?

Once he has setup his narratives, he bridges the gap. Let’s keep in mind that his purpose in these stories are for audience awareness. To teach. We can adapt these narrative¹¹ concepts, though, in communications for other purposes.

Exercise 6 By this discussion, are the Citi Bike and Dodgers memos a story? If not, what they may lack? If so, explain what structure or form makes them a story. Do the story elements — or would they if used — add persuasive effect?

1.3.1.6 Revise for the audience

“We write a first draft for ourselves; the drafts thereafter increasingly for the reader” (J. Williams and Colomb 1990). Revision lets us switch from writing to understand to writing to explain. Switching audience is critical, and not doing so is a common mistake. Schimel (2012) explains one manifestation of the error:

Using an opening that explains a widely held schema is a flaw common with inexperienced writers. Developing scholars are still learning the material and assimilating it into their schemas. It isn’t yet ingrained knowledge, and the process of laying out the information and arguments, step by step, is part of what ingrains it to form the schema. Many developing scholars, therefore, have a hard time jumping over this material by assuming that their readers take it for granted. Rather, they are collecting their own thoughts and putting them down. There is nothing wrong with explaining things for yourself in a first draft. Many authors aren’t sure where they are going when they start, and it is not until the second or third paragraph that they get into the meat of the story. If you do this, though, when you revise, figure out where the real story starts and delete everything before that.

Revision gives us opportunity to focus on our audience once we understand what we have learned. This benefit alone is worth revision.

But it does more, especially when we allow time to pass between revisions: “If you start your project early, you’ll have time to let your revised draft cool. What seems good one day often looks different the next” (Booth et al. 2016a). As you revise, read aloud. While normal conversations do not typically follow grammatically correct language, well-written communications should smoothly flow when read aloud. Try reading this sentence aloud, following the punctuation:

When we read prose, we hear it…it’s variable sound. It’s sound with — pauses. With emphasis. With, well, you know, a certain rhythm (Goodman 2008).

And when revising, consider each word and phrase, and test whether removing that word or phrase changes the context or meaning of the sentence for your audience. If not, remove it. In a similar manner, when choosing between two words with equally precise meaning, it is generally best to use the word with fewer syllables or that flows more naturally when read aloud.

Consider this 124-word blog post for what became a data-for-good project:

Improving Traffic Safety Through Video Analysis

Nearly 2,000 people die annually as a result of being involved in traffic-related accidents in Jakarta, Indonesia. The city government has invested resources in thousands of traffic cameras to help identify potential short-term (e.g. vendor carts in a hazardous location) and long-term (e.g. poorly engineered intersections) safety risks. However, manually analysing the available footage is an overwhelming task for the city’s Transportation Agency. In support of the Jakarta Smart City initiative, our team hopes to build a video-processing pipeline to extract structured information from raw traffic footage. This information can be integrated with collision, weather, and other data in order to build models which can help public officials quickly identify and assess traffic risks with the goal of reducing traffic-related fatalities and severe injuries.

The authors identified their audience explicitly in their award-winning write-up (Caldeira et al. 2018),

We want this project to provide a template for others who hope to successfully deploy machine learning and data driven systems in the developing world. . . . These lessons should be invaluable to the many researchers and data scientists who wish to partner with NGOs, governments, and other entities that are working to use machine learning in the developing world.

Exercise 7 Explain the similarities and differences in structure, categories of information, and level of detail between the above blog post and our two, example memos.

Exercise 8 Explain the similarities and differences you would expect between their audience and the background and experience you would expect from the chief analytics executive for the City of Jakarta.

Exercise 9 For this exercise, your relationship to the chief analytics executive at Jakarta would be that of employee or consultant (your choice). Revise the above blog post into a 250-word memo written to whom you imagine as the chief analytics executive for the City of Jakarta, with the purpose of him or her approving of you moving forward with the project, beginning with a formal proposal. You have the exclusive benefit of their post-project write-up, but don’t use any described actual results in your revisions.

1.3.2 Persuasion

Should we use data science to persuade others? The late Robert Abelson thought so when he published Abelson (1995). But since then, this question has been under the public eye as we try to correct the replication crisis we mentioned in section ??. A special interest group has formed in service of this correction. Wacharamanotham et al. (2018) explains,

we propose to refer to transparent statistics as a philosophy of statistical reporting whose purpose is to advance scientific knowledge rather than to persuade. Although transparent statistics recognizes that rhetoric plays a major role in scientific writing [citing Abelson], it dictates that when persuasion is at odds with the dissemination of clear and complete knowledge, the latter should prevail.

Gelman (2018) poses the question, too:

Consider this paradox: statistics is the science of uncertainty and variation, but data-based claims in the scientific literature tend to be stated deterministically (e.g. “We have discovered … the effect of X on Y is … hypothesis H is rejected”). Is statistical communication about exploration and discovery of the unexpected, or is it about making a persuasive, data-based case to back up an argument?

Only to answer:

The answer to this question is necessarily each at different times, and sometimes both at the same time.

Just as you write in part in order to figure out what you are trying to say, so you do statistics not just to learn from data but also to learn what you can learn from data, and to decide how to gather future data to help resolve key uncertainties.

Traditional advice on statistics and ethics focuses on professional integrity, accountability, and responsibility to collaborators and research subjects.

All these are important, but when considering ethics, statisticians must also wrestle with fundamental dilemmas regarding the analysis and communication of uncertainty and variation.

Gelman seems to place persuasion with deterministic statements and contrasts that with the communication of uncertainty.

Exercise 10 How do you interepret Gelman’s statement? Must we trade uncertainty for persuasive arguments? Discuss these issues and the role of persuasion, if any, in the context of a data analytics project.

1.3.2.1 Methods of persuasion

A means of persuasion “is a sort of demonstration (for we are most persuaded when we take something to have been demonstrated),” writes Aristotle and Reeve (2018). Consider, first, appropriateness of timing and setting, Kairos. Can the entity act upon the insights from your data analytics project, for example? What affect may acting at another time of place mean for the audience? Second, arguments should be based on building common ground between listener and speaker, or listener and third-party actor. Common ground may emerge from shared emotions, values, beliefs, ideologies, or anything else of substance. Aristotle referred to this as pathos. Third, Arguments relying on the knowledge, experience, credibility, integrity, or trustworthiness of the speaker — ethos — may emerge from the character of the advocate or from the character of another within the argument, or from the sources used in the argument. Fourth, the argument from common ground to solution or decision should be based on the syllogism or the syllogistic form, including those of enthymemes and analogies. Called logos, this is the logical component of persuasion, which may reason by framing arguments with metaphor, analogy, and story that the audience would find familiar and recognizable. Persuasion, then, can be understood as researching the perspectives of our audience about the topic of communication, and moving from their point of view “step by step to a solution, helping them appreciate why the advocated position solves the problem best” (Perloff 2017). The success of this approach is affected by our accuracy and transparency.

Exercise 11 In the Citi Bike memo example 1, identify possible audience perspectives of the communicated topic. In what ways, if at all, did the communication seek to start with common ground? Do you see any appeals to credibility of the author or sources? What forms of logic were used in trying to persuade the audience to approve of the request? Consider whether other or additional approaches to kairos, pathos, ethos, and logos could improve the persuasive effect of the communication.

Exercise 12 In the Dodgers memo example 2, identify possible audience perspectives of the communicated topic. In what ways, if at all, did the communication seek to start with common ground? Do you see any appeals to credibility of the author or sources? What forms of logic were used in trying to persuade the audience to take action? Consider whether other or additional approaches to kairos, pathos, ethos, and logos could improve the persuasive effect of the communication.

Exercise 13 In the second Dodgers example — the draft proposal — is the communication approach identical to that in the Dodgers memo? If not, in what ways, if at all, did the communication seek to start with common ground? Do you see any appeals to credibility of the author or sources? What forms of logic were used in trying to persuade the audience to take action? Consider whether other or additional approaches to kairos, pathos, ethos, and logos could improve the persuasive effect of the communication.

Exercise 14 As with the above exercises, examine your draft data analytics memo. Identify how the audience may view the current circumstances and solution to the problem or opportunity you have described. Remember that it tends to be very difficult to see through our biases, so ask a colleague to help provide perspective on your audience’s viewpoint. Have you effectively framed the communication using common ground? Explain.

1.3.2.2 Accuracy

Narrative arguments must avoid any temptation for overstatement. Strunk and White (2000) warn:

A single overstatement, wherever or however it occurs, diminishes the whole, and a carefree superlative has the power to destroy, for readers, the object of your enthusiasm.

Two prominent legal scholars, one a former United States Supreme Court Justice, agree. Scalia and Garner (2008) explain:

Scrupulous accuracy consists not merely in never making a statement you know to be incorrect (that is mere honesty), but also in never making a statement you are not certain is correct. So err, if you must, on the side of understatement, and flee hyperbole. . . Inaccuracies can result from either deliberate misstatement or carelessness. Either way, the advocate suffers a grave loss of credibility from which it is difficult to recover.

As in law, so too in the context of arguments supporting research:

But in a research argument, we are expected to show readers why our claims are important and then to support our claims with good reasons and evidence, as if our readers were asking us, quite reasonably, Why should I believe that?… Instead, you start where your readers do, with their predictable questions about why they should accept your claim, questions they ask not to sabotage your argument but to test it, to help both of you find and understand a truth worth sharing (p. 109)…. Limit your claims to what your argument can actually support by qualifying their scope and certainty (p. 129) (Booth et al. 2016b).

1.3.2.3 Transparency

Edward R. Tufte (2006a) explains, “The credibility of an evidence presentation depends significantly on the quality and integrity of the authors and their data sources.”

Be accurate. Be transparent.

1.3.2.4 Syllogism and enthymeme

Leaving aside emotional appeals [for the moment], persuasion is possible only because all human beings are born with a capacity for logical thought. It is something we all have in common. The most rigorous form of logic, and hence the most persuasive, is the syllogism (Scalia and Garner 2008).

Syllogisms are one of the most basic tools of logical reasoning and argumentation. They are structured argument, constructed with a major premise, a minor premise, and a conclusion. Formally, the structure is of the form,

All A are B.

C is A.

Therefore, C is B.

Such rigid use of “all” and “therefore” isn’t necessary, what’s necessary is the meaning of each premise and conclusion.

We may sometimes abbreviate the syllogism, leaving one of the premises implied (enthymeme). The effectiveness of this approach depends upon whether your audience will, from their knowledge and experience, naturally fill in the implied gap in logic.

Syllogism and enthymeme are a powerful tool for persuasion. But the persuasive effect may be compromised — as tested experimentally, see (Copeland, Gunawan, and Bies-Hernandez 2011) and (Evans, Barston, and Pollard 1983) — by various audience biases and perceptions of credibility, discussed above. Logic also serves as a building block for a rhetoric of narrative, i.e., a narrative that convinces the audience.

1.3.2.5 Narrative as argument

A rhetoric of narrative is logical, but also emotive and ethical (Rodden 2008). It may seem surprising to find argument common in fiction¹², and its value grows with non-fiction and communication for business purposes. A rhetorical narrative functions, if effective, by adjusting its ideas to its audience, and its audience to its ideas. The idea, in this sense, includes the sequence of events that demonstrate change or contrast, introduced in section ??. To enable action on an issue, in Aristotle’s words, dispositio, it was essential to state the case through description — writing imaginable pictures — and narration (telling stories) (Aristotle and Reeve 2018).

Consider our two memo examples 1 and 2. Do either elicit images in the narratives? Explain. In the Citi Bike memo, what might be a reason for quoting Dani Simmons? Does that reason compare with or differ from how you perceive possible reasons for referencing Sandy Koufax in the Dodgers example?

1.3.2.6 Priming and emotion

An introductory story can prime an audience for our main message:

priming is what happens when our interpretation of new information is influenced by what we saw, read, or heard just prior to receiving that new information. Our brains evaluate new information by, among other things, trying to fit it into familiar, known categories. But our brains have many known categories, and judgments about new information need to be made quickly and efficiently. One of the “shortcuts” our brains use to process new information quickly is to check the new information first against the most recently accessed categories. Priming is a way of influencing the categories that are at the forefront of our brains (L. L. Berger and Stanchi 2018).

As we make decisions based on emotion (Damasio 1994), and we may even start with emotion and back into supporting logic (Haidt 2001), we can introduce our messages with emotional priming, too. Yet we should be careful with this approach as audiences may feel manipulated and become resistant — or even opposed — to our message.

1.3.2.7 Tone of an argument

When trying to persuade, authors sometimes approach changing minds too directly:

Many of us view persuasion in macho terms. Persuaders are seen as tough-talking salespeople, strongly stating their position, hitting people over the head with arguments, and pushing the deal to a close. But this oversimplifies matters. It assumes that persuasion is a boxing match, won by the fiercest competitor. In fact, persuasion is different. It’s more like teaching than boxing. Think of a persuader as a teacher, moving people step by step to a solution, helping them appreciate why the advocated position solves the problem best. Persuasion, in short, is a process (Perloff 2017).

Try gradually leading audiences to act, framing your message as more reasonable among options, compromising, or any combination of these. And about those other options for decisions. Showing our audience that our message is more reasonable among options requires discussing those other options. If we do not discuss alternatives, and our audience knows of them or learns of them, they may find our approach less credible, and thus less persuasive, because we did not consider them in advocating our message.

1.3.2.8 Narrative patterns

Stories are built upon narrative patterns (Riche et al. 2018). These include patterns for argumentation, the action or process of reasoning systematically in support of an idea, action, or theory. Patterns for argumentation serve the intent of persuading and convincing audiences. Let’s consider three such patterns: comparison, concretize, and repetition.

Comparison allows the narrator to show equality of both data sets, to explicitly highlight differences and similarities, and to give reasons for their difference. We have already seen various forms of graphical comparison used for understanding. In (Knaflic 2015),, the author offers an example showing graphical comparison to support a call to action, see figure 6.

Figure 6: Knaflic’s example uses comparison to persuade its audience to hire employees.

Concretizing, another type of pattern useful in argumentation, shows abstract concepts with concrete objects. This pattern usually implies that each data point is represented by an individual visual object (e.g., a point or shape), making them less abstract than aggregated statistics. Let’s consider, first, an example from Reuters. In their article Scarr and Hernandez (2019), the authors encode data as individual images of plastic bottles collecting over time, figure 7, also making comparisons between the collections and familiar references, to demonstrate the severity of plastic misuse.

Figure 7: Authors use individual images of bottles to concretize the problem with plastic.

From a persuasive point of view, how does this form of data encoding compare with their secondary graphic, see figure 8, in the same article:

Figure 8: This graphic reports plastic (mis)use graphically and through annotation.

Exercise 15 Do the two graphics intend to persuade in different ways? Explain.

Here’s another example from news, the New York Times. Manjoo (2019) represents each instance of tracking an individual who browsed various websites. Figure 9 represents a snippet from the full information graphic. The full graphic concretizes each instance of being tracked. Notice each colored dot is timestamped and labeled with a location. The intended effect is to convey an overwhelming sense to the audience that online readers are being watched — a lot.

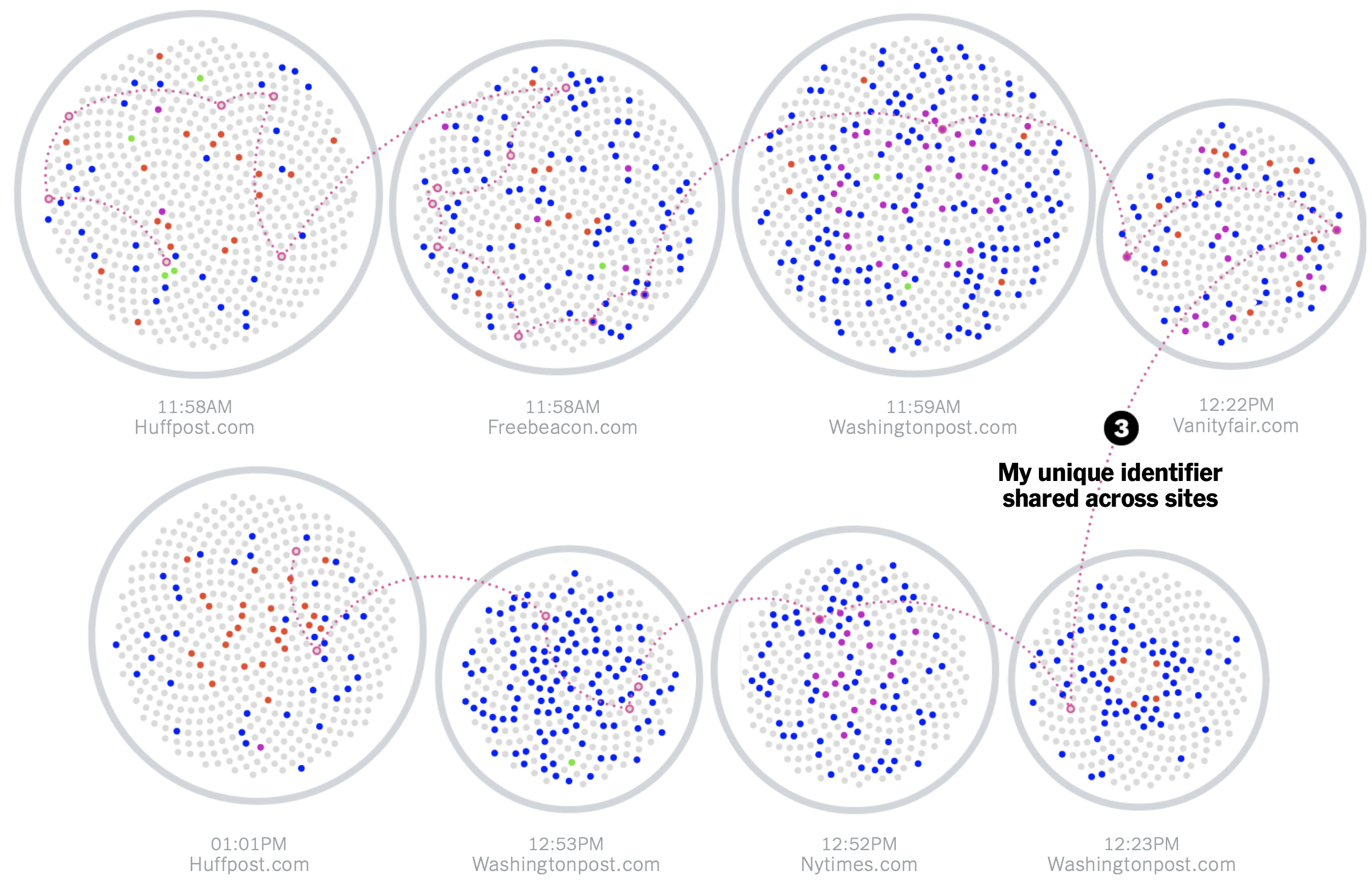
Figure 9: This snippet of the information graphic shows concretizing each instance of tracking someone’s every browser click online to create an overwhelming sense of being watched.

Review the full infographic and consider whether the use of concretizing each timestamped instance, labeled by location, heightens the realization of being tracked more than just reading the more abstract statement that “hundreds of trackers followed me.”

Like concretizing, repetition is an established pattern for argumentation. Repetition can increase a message’s importance and memorability, and can help tie together different arguments about a given data set. Repetition can be employed as a means to search for an answer in the data. Let’s consider another information graphic, which exemplifies this approach. Roston and Migliozzi (2015) uses several rhetorical devices intended to persuade the audience that greenhouse gasses cause global warming. A few of the repeated graphics and questions are shown in figure 10, reproduced from the article.

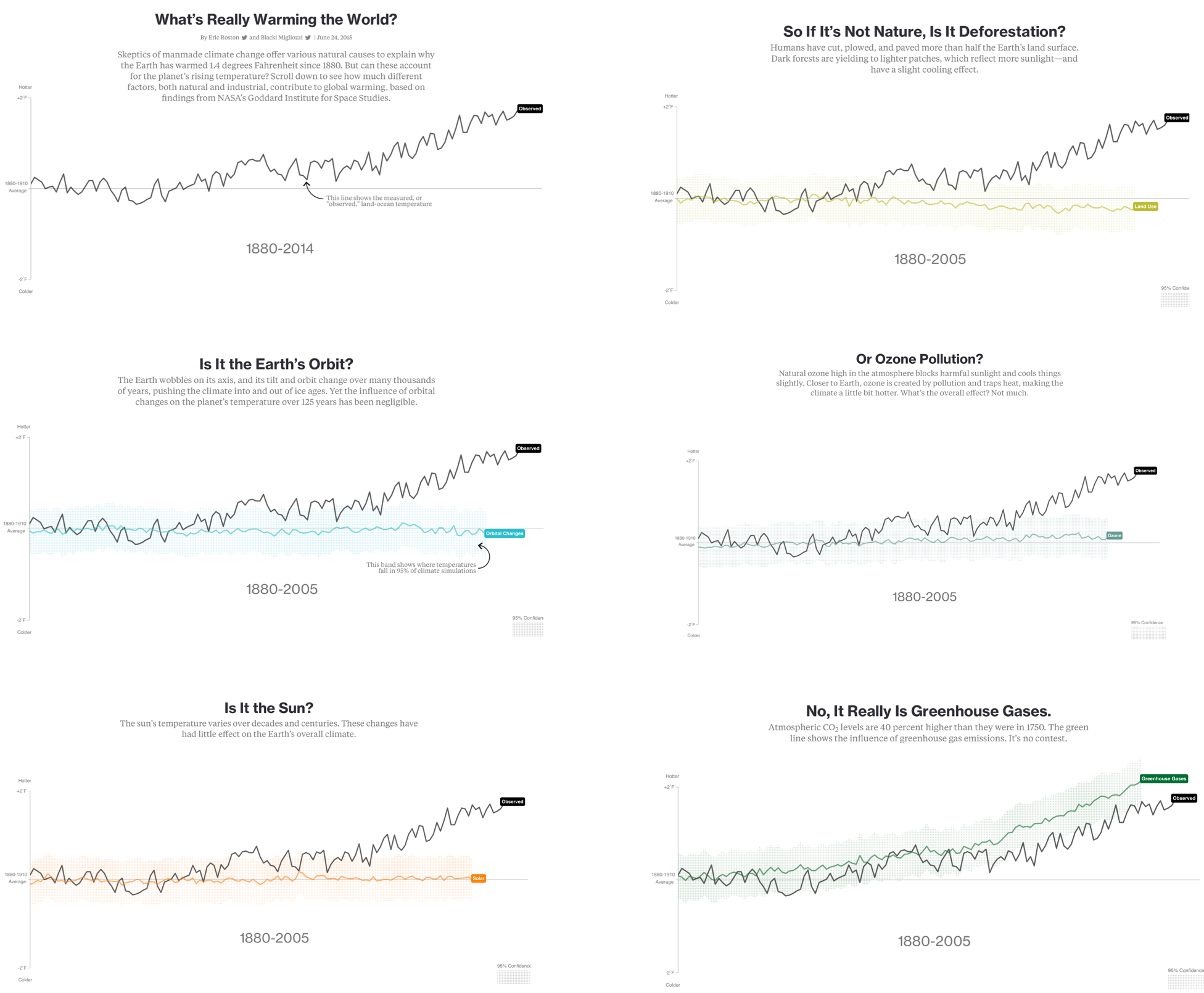
Figure 10: Repetition is used in several ways in this graphic-based news story.

1.3.2.9 Statistical persuasion

Let’s consider, now, how statistics informs persuasion.

1.3.2.9.1 Comparison is crucial

We’ve touched upon the importance of comparison. Edward R. Tufte (2006a) explains the centrality of comparison, “The fundamental analytical act in statistical reasoning is to answer the question ‘Compared with what?’”

Abelson (1995), too, forcefully argues that comparison is central: “The idea of comparison is crucial. To make a point that is at all meaningful, statistical presentations must refer to differences between observation and expectation, or differences among observations.” Abelson tests his argument through a statistical example,

The average life expectancy of famous orchestral conductors is 73.4 years.

He asks: Why is this important; how unusual is this? Would you agree that answering his question requires some standards of comparison? For example, should we compare with orchestra players? With non-famous conductors? With the public? With other males in the United States, whose average life expectancy was 68.5 at the time of the study reported by Abelson? With other males who have already reached the age of 32, the average age of appointment to a first conducting post, almost all of whom are male? This group’s average life expectancy was 72.0.

1.3.2.9.2 Elements of statistical persuasion

Several properties of data, and its analysis and presentation, govern its persuasive force. Abelson describes these as magnitude of effects, articulation of results, generality of effects, interestingness of argument, and credibility of argument: MAGIC.

Magnitude of effects. The strength of a statistical argument is enhanced in accord with the quantitative magnitude of support for its qualitative claim. Consider describing effect sizes like the difference between means, not dichotomous tests. The information yield from null hypothesis tests is ordinarily quite modest, because all one carries away is a possibly misleading accept-reject decision. To drive home this point, let’s model a realization from a linear relationship between two independent, random variables \(\textrm{normal}(x \mid 0, 1)\) and \(\textrm{normal}(y \mid 1, 1)\) by simulating them in R as follows:

set.seed(9)
y <- rnorm(n = 1000, mean = 1, sd = 1)
x <- rnorm(n = 1000, mean = 0, sd = 1)

And model them using a linear regression,

model_fit <- lm(y ~ x)

Results in a “statistically significant” p-value:

	Dependent variable:
	y
x	-0.063** (0.031)
Constant	1.005*** (0.030)
Observations	1,000
R2	0.004
Adjusted R2	0.003
Residual Std. Error	0.959 (df = 998)
F Statistic	4.211** (df = 1; 998)
Note:	p<0.1; p<0.05; p<0.01

Yet we know there is no actual relationship between the two variables. p-values say little, and can mislead. Here’s what a p-value of less than, say, 0.01 means:

If it were true that there were no systematic difference between the means in the populations from which the samples came, then the probability that the observed means would have been as different as they were, or more different, is less than one in a hundred. This being strong grounds for doubting the viability of the null hypothesis, the null hypothesis is rejected.

More succinctly we might say it is the probability of getting the data given the null hypothesis is true: mathematically, \(P(\textrm{Data} \mid \textrm{Hypothesis})\). There are two issues with this. First, and most problematic, the threshold for what we’ve decided is significant is arbitrary, based entirely upon convention pulled from a historical context not relevant to much of modern analysis.

Secondly, a p-value is not what we usually want to know. Instead, we want to know the probability that our hypothesis is true, given the data, \(P(\textrm{Hypothesis} \mid \textrm{Data})\), or better yet, we want to know the possible range of the magnitude of effect we are estimating. To get the probability that our hypothesis is true, we also need to know the probability of getting the data if the hypothesis were not true:

\[ P(\textrm{H} \mid \textrm{D}) = \frac{P(\textrm{D} \mid \textrm{H}) P(\textrm{H})}{P(\textrm{D} \mid \textrm{H}) P(\textrm{H}) + P(\textrm{D} \mid \neg \textrm{H}) P(\neg \textrm{H})} \]

Decisions are better informed by comparing effect sizes and intervals. Whether exploring or confirming analyses, show results using an estimation approach — use graphs to show effect sizes and interval estimates, and offer nuanced interpretations of results. Avoid the pitfalls of dichotomous tests¹³ and p-values. Dragicevic (2016) writes, “The notion of binary significance testing is a terrible idea for those who want to achieve fair statistical communication.” In short, p-values alone do not typically provide strong support for a persuasive argument. Favor estimating and using magnitude of effects. Let’s briefly consider the remaining characteristics that Abelson describes of statistical persuasion. These:

Articulation of results. The degree of comprehensible detail in which conclusions are phrased. This is a form of specificity. We want to honestly describe and frame our results to maximize clarity (minimizing exceptions or limitations to the result) and parsimony (focusing on consistent, connected claims).

Generality of effects. This is the breadth of applicability of the conclusions. Over what context can the results be replicated?

Interestingness of argument. For a statistical story to be theoretically interesting, it must have the potential, through empirical analysis, to change what people believe about an important issue.

Credibility of argument. Refers to believability of a research claim, requiring both methodological soundness and theoretical coherence.

Let’s get back to the ever-important concept of comparison.

In language describing quantities, we have two main ways to compare. One form is additive or subtractive. The other is multiplicative. We humans perceive or process these comparisons differently. Let’s consider an example from Andrews (2019):

The Apollo program crew had one more astronaut than Project Gemini. Apollo’s Saturn V rocket had about seventeen times more thrust than the Gemini-Titan II.

We process the comparative language of “seventeen times more” differently than “1,700 percent more” or “33 versus 1.9”. Add and subtract comparisons are easier for people to understand, especially with small numbers. Relative to additive comparisons, multiplying or dividing are more difficult. This includes comparisons expressed as ratios: a few times more, a few times less. People generally try to interpret multiplying operations through pooling, or repeat addition.

In Andrews’s example, it may be better to show a graphical comparison,

Figure 11: A bar chart allows relative comparisons between quantities that may be generally more useful than merely displaying numbers.

Statistics and narrative.

We’ve discussed narrative and statistics as forms of persuasion. And we’ve seen examples of their combination. Is the combination more persuasive than either individual form? Some researchers have claimed that the persuasive effect depends on the data and statistics. Krause and Rucker (2020) argue from an empirical study that narrative can improve less convincing data or statistics, but may actually detract from strong numerical evidence. Their study involved survey responses from participants that reviewed \(a_1\)) less favorable data (a phone that was relatively heavy and shatter-tested in a 3-foot drop) in the form of a list and \(a_2\)) the same data embedded within a narrative. The data was then changed to be more favorable (a phone that was relatively light and shatter-tested in a 30-foot drop) and \(b_1\)) placed into a list and \(b_2\)) the same, more favorable data was embedded within the same narrative. When comparing responses involving the less-favorable data, the researchers found that the narrative form positively influenced participants relative to presenting the data alone. But when comparing responses involving the more favorable data, the relationship reversed. Respondents was more swayed by the data alone than when presented with it embedded within the narrative. Of note, there was no practical (or significant) difference in responses between narratives with either data. They conclude, from the study, that narratives operate by taking the focus off the data, which may either help or harm a claim, depending on the strength of the data.

But a review of the actual narrative created for the study reveals that the narrative was not about the thing generating the data (a phone and its properties). Instead, the narrative was about a couple hiking that encountered an emergency and used the phone during the emergency. In other words, the data of the phone characteristics amounted to what the advertising industry might call a “product placement.” Product placements, of course, have been found to be effective in transferring sentiment about the narrative to sentiment about the product. But it would be dangerous to generalize from this empirical study to potential effects and operations of other forms of narrative. Instead of choosing between listing convincing data on its own or embedding it as a product placement, we should consider providing narrative context focused on the data and thing that generated it. In other words, we can create a narrative that emphasizes the data, instead of shifting our audiences’ focus from the data. And we can create that narrative context using metaphor, simile, and analogy, discussed next.

1.3.2.10 Comparison through metaphor, simile, analogy

Metaphor adds to persuasiveness by reforming abstract concepts into something more familiar to our senses, signaling particular aspects of importance, memorializing the concept, or providing coherence throughout a writing¹⁴. The abstract concepts we need help explaining, ideas we need to make important, or the multiple ideas we need to link, we call the target domain. Common source domains include the human body, animals, plants, buildings and constructions, machines and tools, games and Sport, money, cooking and food, heat and cold, light and darkness, and movement and direction. Let’s consider some examples.

In a first example, we return to Andrews (2019). As a book-length communication, it has more space to build the metaphor, and does so borrowing from the source domain of music:

How do we think about the albums we love? A lonely microphone in a smoky recording studio? A needle’s press into hot wax? A rotating can of magnetic tape? A button that clicks before the first note drops? No!

The mechanical ephemera of music’s recording, storage, and playback may cue nostalgia, but they are not where the magic lies. The magic is in the music. The magic is in the information that the apparatuses capture, preserve, and make accessible. It is the same with all information.

After setting up this metaphor, he repeatedly refers back to it as a form of shorthand each time:

When you envision data, do not get stuck in encoding and storage. Instead, try to see the music. … Looking at tables of any substantial size is a little like looking at the grooves of a record with a magnifying glass. You can see the data but you will not hear the music. … Then, we can see data for what it is, whispers from a past world waiting for its music to be heard again.

What, if anything, do you think use of this source domain adds to the audiences understanding of data and information? For other uses of simile and metaphor for data analytics concepts, see McElreath (2020), using mythology (a golem) to represent properties of statistical models, Rosenbaum (2017), using poetry about a road not taken, Frost (1921) to explain how we think about, and the properties of, co-variates.

Exercise 16 Find other examples of metaphor and simile used to describe data science concepts. Do you believe they aide understanding for any particular audience(s)? Explain.

1.3.2.11 Patterns that compare, organize, grab attention

We can use patterns to “make the words they arrange more emphatic or memorable or otherwise effective” (Farnsworth 2011). In Classical English Rhetoric, Farnsworth provides a wealth of examples, categorized. Unexpected word placement calls attention to them, creates emphasis by coming earlier than expected or violating the reader’s expectations. Note that, to violate expectations necessarily means reserving a technique like inversion for just the point to be made, lest the reader come to expect it — more is less, less is more. Secondly, it can create an attractive rhythm. Thirdly, when the words that bring full meaning come later, it can add suspense, and finish more climactic.

These patterns can be the most effective and efficient ways to show comparisons and contrasts. While Farnsworth provides a great source of these rhetorical patterns in more classical texts, we can find plenty of usage in something more relevant to data science. In fact, we have already considered a visual form of repetition in section ??. Let’s consider example structure (reversal of structure, repetition at the end) used in another example text for data science, found in Rosenbaum (2017):

A covariate is a quantity determined prior to treatment assignment. In the Pro-CESS Trial, the age of the patient at the time of admission to the emergency room was a covariate. The gender of the patient was a covariate. Whether the patient was admitted from a nursing home was a covariate.

The first sentence begins “A covariate is …” Then, the next three sentences reverse this sentence structure, and repeat to create emphasis and nuance to the reader’s understanding of a covariate. Here’s another pattern (Repetition at the start, parallel structure) from Rosenbaum’s excellent book:

One might hope that panel (a) of Figure 7.3 is analogous to a simple randomized experiment in which one child in each of 33 matched pairs was picked at random for exposure. One might hope that panel (b) of Figure 7.3 is analogous to a different simple randomized experiment in which levels of exposure were assigned to pairs at random. One might hope that panels (a) and (b) are jointly analogous to a randomized experiment in which both randomizations were done, within and among pairs. All three of these hopes may fail to be realized: there might be bias in treatment assignment within pairs or bias in assignment of levels of exposure to pairs.

Repetition and parallel structure are especially useful where, as in these examples, the related sentences are complex or relatively long. Let’s consider yet another pattern (asking questions and answering them):

Where did Fisher’s null distribution come from? From the coin in Fisher’s hand.

Rhetorical questions or those the author answers are a great way to create interest when used sparingly. In your own studies, seeing just a few examples invites direct imitation of them, which tends to be clumsy when applied. Immersion in many examples, however, allows them to do their work by way of a subtler process of influence, with a gentler and happier effect on our resulting style of narrative.

1.3.2.12 Le mot juste — the exact word

Writing poetically, Goodman (2008) explains the importance of finding the exact word. Le mot juste, in French, is how it’s expressed.

In our search we must also keep in mind, and use, words with the appropriate precision, as Alice explains:

“When I use a word,” Humpty Dumpty said in rather a scornful tone, “it means just what I choose it to mean—nothing more nor less.”

“The question is,” said Alice, “whether you can make words mean so many different things” (Carroll 2013).

Yet empirical studies suggest variation in our understanding of words that express quantity. For words meant to convey quantity, their meanings vary more than Alice would like. Barclay et al. (1977) reports survey responses from 23 NATO military officers who were asked to assign probabilities to particular phrases if found in an intelligence report. In another, online survey of 46 individuals, zonination (2015) provided responses to the question: What [probability/number] would you assign to the phrase [phrase]? where the phrases matched those of the NATO study. The combined responses in figure 12 show wide variation in what probabilities individuals associate with words, although some ordering or ranking is evident.

Figure 12: Results from the combined studies reflect uncertainty in the probability that people associate with words.

As with variation in probabilities assigned to words about uncertainty, the empirical study suggests variation in amounts assigned to words about size, shown in Figure 13.

Figure 13: Even words whose definitions refer to counts have significant variation in perceived meaning.

Variance in perception of the meaning of such words does not imply we should avoid them altogether. It does mean, however, we should be aware of the meaning others may impart and complement our use of them with numerals or graphic displays.

1.3.3 Heuristics and biases

Humans have two separate processes for understanding information, which Kahneman (2013) labels as system one and system two. If we are to find common ground, and move our audience to a new understanding for decisionmaking, we must understand how they think. Intuitive (system one) thinking — impressions, associations, feelings, intentions, and preparations for actions — flow effortlessly. This system mostly guides our thoughts, as illustrated next. Most of us immediately sense emotion from the face below, system one processing, but would need to work hard to mentally calculate 17 x 24, system two processing.

System one uses heuristics, biases. Reflective (system two) thinking, in contrast, is slow, effortful, and deliberate. Both systems are continuous, but system two typically monitors things, and only steps in when stakes are high, we detect an obvious error, or rule-based reasoning is required. For a sense of this difference, Kahneman provides exemplary information that we process using system one, as in the above image, and system two, as in mentally calculating 17 x 24. For other examples, consider figure 7 (system one) and figure 8 (processing may depend on familiarity with the graphic — a alluvial diagram — and which comparisons are of focus within the graphic).

On how humans process information, we have decades of empirical and theoretical research available (Gilovich, Griffin, and Kahnman 2009), and theoretical foundations have long been in place (J. B. Miller and Gelman 2020).

Kahneman, Lovallo, and Sibony (2011) gives executives ways to guard against some biases by asking questions and recommending actions:

self-interested biases | Is there any reason to suspect the team making the recommendation of errors motivated by self-interest? Review the proposal with extra care, especially for over optimism.

the affect heuristic | Has the team fallen in love with its proposal? Rigorously apply all the quality controls on the checklist.

groupthink | Were there dissenting opinions within the team? Were they explored adequately? Solicit dissenting views, discreetly if necessary.

saliency bias | Could the diagnosis be overly influenced by an analogy to a memorable success? Ask for more analogies, and rigorously analyze their similarity to the current situation.

confirmation bias | Are credible alternatives included along with the recommendation? Request additional options.

availability bias | If you had to make this decision in a year’s time, what inform-ation would you want, and can you get more of it now? Use checklists of the data needed for each kind of decision.

anchoring bias | Where are the numbers from? Can there be … unsubstantiated numbers? … extrapolation from history? … a motivation to use a certain anchor? Re-anchor with data generated by other models or benchmarks, and request a new analysis.

halo effect | Is the team assuming that a person, organization, or approach that is successful in one area will be just as successful in another? Eliminate false inferences, and ask the team to seek additional comparable examples.

sunk-cost fallacy, endowment effect | Are the recommenders overly attached to past decisions? Consider the issue as if you are a new executive.

overconfidence, optimistic biases, competitor neglect | Is the base case overly optimistic? Have a team build a case taking an outside view: use war games.

disaster neglect | Is the worst case bad enough? Have the team conduct a premortem: imaging that the worst has happened, and develop a story about the causes.

loss aversion | Is the recommending team overly cautious? Align incentives to share responsibility for the risk or to remove risk.

We increase persuasion by addressing these issues in anticipation that our audience will want to know. It’s very hard to remain aware of our own biases, so we need to develop processes that identify them and, most importantly, get feedback from others to help protect against them. Get colleagues to help us. Present ideas from a neutral perspective. Becoming too emotional suggests bias. Make analogies and examples comparable to the proposal. Genuinely admit uncertainty in the proposal, and recognize multiple options. Identify additional data that may provide new insight. Consider multiple anchors in a proposal.

1.4 Integrating Text and Data

1.4.1 Layout, hierarchy, and integration

Visual presentation is communication.

1.4.1.1 Typography

For visual presentation of communication, we may first think about a data graphic. But consider this paragraph from Strunk and White (2000), white space removed:

Vigorouswritingisconcise.Asentenceshouldcontainnounnecessarywords,aparagraphnounnecessarysentences,forthesamereasonthatadrawingshouldhavenounnecessarylinesandamachinenounnecessaryparts.Thisrequiresnotthatthewritermakeallhissentencesshort,oravoidalldetailandtreatsubjectsonlyinoutline,butthateverywordtell.Asingleoverstatement,whereverorhoweveritoccurs,diminishesthewhole,andacarefreesuperlativehasthepowertodestroy,forreaders,theobjectofyourenthusiasm.

The visual presentation of communication involves all best practices in typography and design. Adding white space between words, just one of many components of typography, is an obvious decision. It makes the advice from Strunk and White¹⁵ more readable, more understandable:

Vigorous writing is concise. A sentence should contain no unnecessary words, a paragraph no unnecessary sentences, for the same reason that a drawing should have no unnecessary lines and a machine no unnecessary parts. This requires not that the writer make all his sentences short, or avoid all detail and treat subjects only in outline, but that every word tell. A single overstatement, wherever or however it occurs, diminishes the whole, and a carefree superlative has the power to destroy, for readers, the object of your enthusiasm.

Best practices in visual presentation of communication go well beyond spacing between words. Butterick (2018) credits a great deal to, among others, Bringhurst (2004), explaining best practices, well, best. Typography is the visual component of the written word. “Typography is for the benefit of the reader”:

Most readers are looking for reasons to stop reading. . . . Readers have other demands on their time. . . . The goal of most professional writing is persuasion, and attention is a prerequisite for persuasion. Good typography can help your reader devote less attention to the mechanics of reading and more attention to your message.

The typographic choices in the PDF versions of our memo examples 1 and 2 and proposal follow Butterick (2018)’s advice:

Figure 14: Basic typographic guidelines as implemented in examples.

Those best practices do more than aid readability. Experiments have demonstrated that “high quality typography can improve mood [of the reader]” (Larson and Picard 2005), and the better their mood, the more likely they are to consider what you say.

Butterick’s recommendations, and as implemented in the example memos, are designed functionally. When designing communications for the interwebs, also consult Rutter (2017). There will be occasions, however, when more creativity can be used in combination with functionality. Information graphics are an example. You may find inspiration in de Bartolo, Coles, and Spiekermann (2019), which studies the creative placement of text. Not just for text, typography — layout — is for all communication: text, numbers, data graphics, and images.

1.4.1.2 Laying out numbers: tables

Stand-alone numbers should generally fit in the context of a sentence. When reporting multiple numbers, though, consider a table within a paragraph to aid comparisons (Edward R. Tufte 2001b).

Tables require design. Text and numbers are best when aligned to an invisible grid that creates negative or white space between columns and other components of the table. Invisible is key, as grid lines between all rows and columns detract from the data Wong (2013). (Wainer 2016a) works through an example series of tables for multivariate comparisons, and considers its design, data transformations, and organization to aid audience understanding.¹⁶ Along with Tufte, Wainer, and Wong, J. E. Miller (2015) provides us another great resource for advice on creating, and showing examples of, tables.

R. L. Harris (1999) names and describes the components of a typical table, not all of which are always used or if used should be visible:

Figure 15: Basic components of a table.

The better designed tables will minimize any markings other than the data and annotations explaining the data, relying on Gestalt (a subset of design) principles, two¹⁷ of which are proximity and similarity. The Gestalt principle of proximity reflects that we perceive markings closer together — relative to other markings — as belonging to the same group.

Figure 16: Gestalt principles of proximity: can perceive the left group of dots as grouped horizontally and the right group of dots grouped vertically simply based on relative proximity to one another.

As with proximity, we can create the perception of groupings based on similarity of color, or shape, or another attribute. Here’s an example in which the horizontal spacing and vertical spacing are equal to demonstrate the color attributes ability to group:

Figure 17: Gestalt principle of similarity can help us create perceived groups too. In this example, the dots have equal horizontal and vertical spacing, but use different shades.

Consider these Gestalt principles at work in this example table:

Notice the components, think about the underlying grid system organizing the content, the alignment and position of each type of information, and how proximity and similarity help to separate these different information types.

Along with placing numbers in text — sentences — or in tables, we can re-organize them into a hybrid form, having attributes of a table and a graph. This hybrid, called a stem-and-leaf diagram, has attributes of a table because it is constructed with actual numbers, just more compactly than a pure table. It’s also like a graphic in that its profile conveys distributional information similar to a histogram. Figure 18 below provides an example, which is interactive, too. Hover your cursor over a number amongst the “leaves” for instructions interpreting the number:

Figure 18: 5 | 4 represents 54. This stem-and-leaf diagram provides more information than it’s modern replacement, the histogram, in a way more compactly than a table. Hover your cursor over a leaf to show the value represented by the stem and leaf. The representation can be confusing for audiences to whom this is unfamiliar.

R. L. Harris (1999) thoroughly explains variations on stem-and-leaf diagrams.

1.4.1.3 Grid systems and narrative layout

Another aspect of typography and design rely on grid systems. A very basic grid is shown in figure 14, some of its components drawn in brown and labeled in gray: gutters, module, and margin. The gutters between the gridlines create white space that separate information placed into columns, rows, modules, or spatial zones (a spatial zone comprises multiple modules or rows or columns). Of course, the grid lines are not part of the final communication; we create them temporarily to layout and align information. That layout is informed by visual perception and the way we process information in a given culture. When reading English, for example, we generally start processing the information from the top, left, our eyes scanning to the right, and then returning left and down, in a repeating zig-zag pattern. Hebrew is right to left. We call this type of narrative structure linear (Koponen and Hildén 2019). And various graphic design choices can purposefully or inadvertently guide the reader through the material in other ways. Images, unlike sentences, create an open narrative structure, allowing us to reason differently (Koponen and Hildén 2019). We’ll come back to this concept.

Grid systems can be much more complex. We are guided by Muller-Brockmann in his seminal reference, “Arranging surfaces and spaces into a grid creates conformity among texts, images and diagrams. The size of each implies its importance. Reducing elements in a grid suggests planning, intelligibility, clarity, and orderliness of design. One grid allows many creative ways to show relationships” (Müller-Brockmann 1996). A grid with 8 rows by 4 columns and gutter spacing between the blocks, for example, can lead to numerous arrangements of disparate, but related, information:

Yet the commonly aligned sides of word blocks, images, and data graphics can help connect related information. By connect, we mean the layout creates or enables a path that the audience’s eye follows, a scan path. In this paragraph of text, you started reading at its beginning and followed horizontally until the end of the line, then scanned to the left beginning of the line below and repeated the process. In strip comics, the sequentially arranged images encourage a similar linear narrative. But other layouts enable an open narrative. These include radial layouts in which the order we scan relies on focal points, which are prominent components due to, say, their size or color in relation to the surrounding information. Of note, in some circumstances we my intend a serial narrative within an open narrative. Consider labeling or numbering the features, using gestalt principles, or both, to guide the audience.

Thus, as Müller-Brockmann (1996) explained, grids enable orderliness, adds credibility to the information, and induces confidence. Information presented with clear and logically set out titles, subtitles, texts, illustrations and captions will not only be read more quickly and easily but the information will also be better understood.

Exercise 17 Try to identify placement of the (invisible) grid lines used to align information in the Dodgers proposal, which is primarily text.

Exercise 18 Consider the poster version of the information graphic Bremer (2016). Try to identify placement of the (invisible) grid lines used for alignment.

1.4.2 Combined meaning of words and images

Words, graphics, and images — when combined — can provide some extent what Doumont (2009d) prescribed: effective redundancy. This is sometimes called dual coding. And to maximize their combination, we first consider that we process languages and images differently (Ware 2020). Words are read, and processed in linear fashion, serially, one after the other. Images, on the other hand, can be processed or understood as a whole, in parallel.

Secondly, each type of medium conveys meaning differently; neither exactly overlap: a description of an image never actually represents the image. Rather, … it is a representation of thinking about having seen a picture — it’s already formulated in its own terms (Sousanis 2015), paraphrasing (Baxandall 1985). Each is better at conveying certain types of messages. Sousanis puts it: “while image is, text is always about.” Text is usually better for expressing abstract concepts, and procedure, such as logic or programming. Diagrams help when explaining structural relationships.

We can benefit from various studies into the interplay of words and images found in comics, (Cohn 2016); (Sousanis 2015); (McCloud 1993), and extrapolate those concepts into information visualization. Done right, each informs and enriches the other. Images and graphics also enable a unique form of comparison, juxtaposing one image or encoding to another — or to the absence of another — to form meaning.

1.4.3 Visually integrating graphics and text

Good design and typography also enable visual connections between words and sentences to, say, data graphics. Edward R. Tufte (2001b) explains, at their best, graphics are instruments for reasoning about quantitative information. Often the most effective way to describe, explore, and summarize a set of numbers—even a very large set—is to look at pictures of those numbers. Furthermore, of all methods for analyzing and communicating statistical information, well-designed data graphics are usually the simplest and at the same time the most powerful. And if “a means of persuasion is a sort of demonstration,” and we now agree with Aristotle that it is, then graphics are frequently the most effective way to demonstrate things, especially for understanding patterns and comparisons.

But it isn’t a Hobson’s choice, words or graphics. Instead, we should use both. Edward R. Tufte (2001b) explains how they work together: “The principle of data/text integration is: data graphics are paragraphs about data and should be treated as such.”

Visual displays may be integrated directly within the text. Tufte’s book is a living example, and explains the approach:

We were able to integrate graphics right into the text, sometimes into the middle of a sentence, eliminating the usual separation of text and image — one of the ideas Visual Display advocated.

Experiments support Tufte’s advice. Koponen and Hildén (2019) summarizes an experiment of eye-tracking movements and comprehension when reading communications in various layouts (Holsanova, Rahm, and Holmqvist 2006), from which we learned that layouts integrating images within text columns improve communication over both radial layouts and layouts that separate text from images. The integrated approach promoted careful reading of the text between images while layouts separating text from images promoted the reading of a title, skipping the body text, and focusing on the images. Radial layouts were reviewed more quickly than linear, integrated text-image layouts, and less information was retained.

For effective integration, visual display need only be large enough to clearly convey the information as intended for our audience in the manner to be consumed. To make the point, consider the word-sized graphics Edward R. Tufte (2006a) calls sparklines:

.¹⁸ Also note that when the graphic is large enough to include annotation,

The principle of text/graphic/table integration also suggests that the same typeface be used for text and graphic and, further, that ruled lines separating different types of information be avoided.

Exercise 19 Locate two or three narratives with data graphics as paragraphs that you believe the graphic helped persuade audiences of the point of the narrative. Explain why the graphic explained better than words as used.

1.4.4 Annotating data graphics with words

Annotations add explanations and descriptions to introduce the graph’s context, which is important for almost any audience. Annotation plays a crucial role in asynchronous data storytelling as the surrogate for the storyteller. They can also explain how to read the graph, which helps readers unfamiliar with the graph — whether a simple line chart or an advanced technique like a treemap or scatterplot. When done right, the annotation layer will not get in the way for experienced users. Consider, for example, figure 19.

Figure 19: Example of data graphic containing annotation to assist the audience.

From a cognitive perspective, Ware writes that “plac[ing] explanatory text as close as possible to the related parts of a diagram, and us[ing] a graphical linking method” will “reduce [the] need to store information temporarily while switching back and forth between locations” (Ware 2020). Figure 19, published in newspaper article Schleuss and Lin II (2013), displays a scatter plot that encodes the rate change of crime on the x-axis, change of property crime on the y-axis, and rate of crimes as size of the location or point. Note the plot is segmented into quadrants, color-coded to indicate better and worse conditions, and annotations are overlain that explain how to interpret the meaning of a data point located within quadrants of the graphic. The various annotations greatly assist its general audience in decoding the data and considering insights.

Rahlf (2019) provides over 100 examples of annotating and modifying exploratory graphics for presenting in communication., and should be consulted along with this text’s section ??.

1.4.5 Visually linking words with graphics

Placement of data graphics within words and annotating graphics with words are the first step in integrating the information. Another best practice includes using color encodings and other explicit markings, linking words to encodings, such as adding lines connecting related information (Riche et al. 2018):

The link between the narrative and the visualization helps the reader discern what item in the visualization the author is referencing in the text. Create links with annotation, color, luminosity, or lines.

For example, color words in annotations on a data graphic and in the paragraphs surrounding that graphic with the same hue as used in the data encodings of the graphic. This follows the principle of similarity, discussed earlier. Let’s consider an example table, the example we created in section ??, placing it into a paragraph and linking its data to surrounding words (a form of data display):

---

Using Table 1, we can calculate the value of a strike by subtracting the expected run value of a strike, given the game state and count, from the value of a ball, starting from the same game state and count. Let’s say there is a runner on first and second with one out, and the count is 1 ball, 1 strike, suggesting we should expect 0.99 more runs this inning:

Assuming the batter doesn’t swing on the next pitch, a strike lowers expected runs to 0.86 while a ball raises it to 1.11. Thus, in this scenario, the expected value of a strike would be 0.86 - 1.11, or -0.25 runs.

---

Consider the ways we apply the principles of proximity and similarity. Does in-paragraph placement (proximity) and text-data coloring (similarity) help us in learning to use the table? For other examples, see Kay (2015), which provides example uses of color for linking words to data encodings. Yet for another great example of linking paragraphs with illustrations, see Byrne’s revision of Euclid’s first six books (Byrne 2017).

1.4.6 Linking multiple graphics

If individual graphs reveal information and structure from the data, an ensemble of graphs can multiply the effect. By ensemble, we mean multiple graphs simultaneously displayed, each containing different views of the data with common information linked together by various techniques. We’ve already seen one form of an interactive linkage between two graphics in figure 1, which dynamically linked each baseball stadium field boundary to the corresponding fence. And while Cleveland (1985) describes “brushing and linking” — where items selected in on one visual display highlights the same subset of observations in another visual display — as an interactive tool, he effectively shows the technique by highlighting the same data across static displays. Authors Unwin and Valero-Mora (2018) provide a nice example, walking through use of ensembles in exploring data quality, comparing models, and presenting results. As the authors explain,

Coherence in effective ensembles covers many different aspects: a coherent theme, a coherent look, consistent scales, formatting, and alignment. Coherence facilitates understanding.

The additional effort for coherence “are more design than statistics, but they are driven by the statistical information to be conveyed, and it is therefore essential that statisticians concern themselves with them.” Along with using the same theme styles, their choice of placement is informed by best practices in graphic design, which apply a grid system, already discussed.

We’ve covered a lot of material. We can use all these techniques to help in writing a brief proposal to a chief analytics officer, asking him or her to approve our analytics project. Recall the Dodgers memo, example 2? Let’s continue that example with a 750-word brief proposal, see Spencer (2019b). To assess whether the example proposal accomplishes its goals, note the audience. As previously explained, his background includes a doctor of philosophy in Statistics, and experience with machine learning and statistical programming in R.

Exercise 20 Try to identify the document structure in the example brief proposal. Does it identify problems and goals? Data? Methods? Compare the structure, specificity and level of detail to both the memos, examples 1 and 2. Next, consider the tools we’ve covered in business writing, starting with messages and goals, applying typographic best practices, aligning information with grids, integrating graphics within paragraphs, linking words and graphics, annotation, and use of comparison, metaphor, patterns, and examples or analogies to persuade. How many can you find? If you were the director would you be persuaded to approve of the project? Why or why not? How might you edit the proposal to make it more persuasive?

2 Visual

2.1 Visual design and perceptual psychology

The value of data graphics can be grasp from a brief analysis of the following four datasets (1-4) of (x, y) data in table 1 from a famous data set:

Table 1: These four simple datasets are known as Anscombe’s Quartet.

1		2		3		4
x	y	x	y	x	y	x	y
10	8.04	10	9.14	10	7.46	8	6.58
8	6.95	8	8.14	8	6.77	8	5.76
13	7.58	13	8.74	13	12.74	8	7.71
9	8.81	9	8.77	9	7.11	8	8.84
11	8.33	11	9.26	11	7.81	8	8.47
14	9.96	14	8.10	14	8.84	8	7.04
6	7.24	6	6.13	6	6.08	8	5.25
4	4.26	4	3.10	4	5.39	19	12.50
12	10.84	12	9.13	12	8.15	8	5.56
7	4.82	7	7.26	7	6.42	8	7.91
5	5.68	5	4.74	5	5.73	8	6.89

For most of us, reviewing the table for comparing the four datasets from Anscombe (1973) is cognitively taxing, and especially when scanning for differences in the relationships between x and y across datasets. Processing the data this way occurs sequentially; we review data pairs with focused attention. And, here, summary statistics do not differentiate the datasets. All x variables share the same mean and standard deviation (table 2). So do all y variables.

Table 2: The mean and standard deviation per dataset are identical.

	1		2		3		4
	x	y	x	y	x	y	x	y
mean	9.00	7.50	9.00	7.50	9.00	7.50	9.00	7.50
sd	3.32	2.03	3.32	2.03	3.32	2.03	3.32	2.03

Further, the linear regression on each dataset (table 3) suggests that the (x, y) relationship across datasets are the same. Are they?

Table 3: Linear regression coefficients across datasets are practically identical.

Parameter	Mean	Std Err	t-val	p-val
Dataset 1
(Intercept)	3.000	1.125	2.667	0.026
x	0.500	0.118	4.241	0.002
Dataset 2
(Intercept)	3.001	1.125	2.667	0.026
x	0.500	0.118	4.239	0.002
Dataset 3
(Intercept)	3.002	1.124	2.670	0.026
x	0.500	0.118	4.239	0.002
Dataset 4
(Intercept)	3.002	1.124	2.671	0.026
x	0.500	0.118	4.243	0.002

A well-crafted visual display, however, can instantly illuminate any differing (x, y) relationships among the datasets. To demonstrate, we arrange four scatterplots in figure 20 showing the relationships between (x,y), one for each dataset. Overlain on each, we show the linear regression calculated above.

Figure 20: The differing (x, y) relationships among datasets in Anscombe’s Quartet become instantly clear when visualized.

As the example shows, exploratory data analysis using visual and spatial representations add understanding. It allows us to find patterns in data, detecting or recognizing the geometry that encodes the values, assembling or grouping these detected elements, and estimating the relative differences between two or more quantities (Cleveland 1985); (Cleveland 1993). In estimating, we first discriminate between data: we judge whether \(\textbf{a}\) is equal to \(\textbf{b}\). Then we rank the values, judging whether \(\textbf{a}\) is greater than, less than, or equal to \(\textbf{b}\). Finally, we consider the ratio between them using encoded geometries (e.g., relative distance from a common line). Unlike with sequential processing required for table lookups, pattern recognition — and outliers from those patterns — seem to occur in parallel, quickly because we are attuned to preattentive attributes (Ware 2020).

2.1.1 Reasoning with images

We previously mentioned how, unlike processing text in linear fashion, images enable an open narrative, which we process differently (Koponen and Hildén 2019); (Sousanis 2015); (Kosslyn, Thompson, and Ganis 2006); (Baxandall 1985).

We may also combine linear and open narrative structures in various ways (Segel and Heer 2010).

…

2.1.2 Components of a graphic

Graphics include a coordinate system, arranged spatially, and have numerous attributes that we may make visible in some way, if it helps users understand the graphic. These components can be understood in two categories. Those encoding data (data-ink) and all the rest (non-data-ink).

2.1.2.1 Non-data-ink

We’ll use an R/ggplot implementation of graphics to discuss these components¹⁹. Figure \(\ref{fig:nondataink}\) shows the names for most of the non-data-ink components of a visual display.

Figure 21: Edward Tufte advocates maximizing the data-ink ratio within reason. Some non-data-ink can be critical to understanding the data. For each element’s marking, coloring, size, shape, orientation, or transparency setting, ask whether it maximizes our audience’s understanding of the intended insight.

Most of the aesthetics of each labeled component can be set, modified, or removed using the ggplot function theme(), which takes plot components as parameters. We set parameters equal to other formatting functions like, say, element_text() for formatting its typography, element_rect() for formatting its various shape or coloring information, or element_blank() to remove entirely the element. In Figure \(\ref{fig:nondataink}\), for example, we set the panel border attribute linetype and color using,

theme(panel.border = element_rect(color = "gray60", 
                                  linetype = "dashed", 
                                  fill = NA))

We can use the ggplot function annotate() to include words or draw directly onto the plotting area. Figure 22 shows the basic code structure.

Figure 22: GGplot’s functions are set up as layers. We may use more than one geometry or annotation.

In the pseudocode of figure 22, we map variables in the data to aesthetic characteristics of a plot that we see through mapping = aes(<aesthetic> = <variable>)²⁰. Particular aesthetics depend on the type of geometric encoding we choose. A scatter plot, say, would at least include x and y aesthetics. The geometric encodings are created through functions named for their geometries: e.g., geom_point(<...>) for the scatter plot, which we generalize to geom_<type>(<...>). The geometry is then mapped onto a particular coordinate system and scale: coord_<type>(<...>) and scale_<mapping>_<type>(<...>), respectively. Finally, we annotate and label the graph. These can be thought as layers that are added (+) over each previous layer.

The remaining markings of a graphic are the data-ink, the data encodings, discussed next.

2.1.2.2 Data-ink

Encodings depend on data type, which we introduced in section ??. As Andrews (2019) explains, “value types define how data is stored and impact the ways we turn numbers into information.” To recap, these types are either qualitative (nominal or ordered) or quantitative (interval or ratio scale).

“A component is qualitative” and nominal, Bertin²¹ explains, “when its categories are not ordered in a universal manner. As a result, they can be reordered arbitrarily, for purposes of information processing” (Bertin 2010). The qualitative categories are equidistant, of equal importance. Considering Citi Bike, labeled things such bikes and docking stations are qualitative at the nominal level.

“A component is ordered, and only ordered, when its categories are ordered in a single and universal manner” and “when its categories are defined as equidistant.” Ordered categories cannot be reordered. The bases in baseball are ordinal, or ordered: first, second, third, and home. Examples of qualitative ordering may be, say, temporal: morning, noon, night; one comes before the other, but we would not conceptually combine morning and night into a group of units.

When we have countable units on the interval level, the data of these counts are quantitative. A series of numbers is quantitative when its object is to specify the variation in distance among the categories. We represent these numerically as integers. The number of bike rides are countable units. The number of stolen bases in baseball are countable units. We represent these as integers.

Finally, ratio-level, quantitative values represent countable units per countable units of something else. The number of bike rides per minute and the number of strike outs per batter would be two examples, represented as fractions, real numbers.

The first and most influential structural theory of statistical graphics is found the seminal reference, Bertin (1983).

Based on Bertin’s practical experience as a cartographer, part one of this work is an unprecedented attempt to synthesize principles of graphic communication with the logic of standard rules applied to writing and topography.

Part two brings Bertin’s theory to life, presenting a close study of graphic techniques, including shape, orientation, color, texture, volume, and size, in an array of more than 1,000 maps and diagrams. Here are those encoding types:

Figure 23: Bertin’s illustration of the possible encoding forms for data.

Less commonly discussed is Bertin’s update (Bertin 2010) to his original work. In the update, after defining terms he reviews the natural properties of a graphic image. The essence of the graphic image is described in three dimensions. The first two describe spatial properties (e.g. x and y axes) while the third dimension (denoted z) encodes the characteristics of each mark — e.g. size, value, texture, color, orientation, shape — at their particular spatial (x, y) locations.

Bertin’s ideas, over 50-years old, have proven reliable and robust (MacEachren 2019); (Garlandini and Fabrikant 2009).

2.1.2.3 Grammar

Graphics are not charts, explains Wilkinson (2005):

We often call graphics charts. There are pie charts, bar charts, line charts, and so on. [We should] shun chart typologies. Charts are usually instances of much more general objects. Once we understand that a pie is a divided bar in polar coordinates, we can construct other polar graphics that are less well known. We will also come to realize why a histogram is not a bar chart and why many other graphics that look similar nevertheless have different grammars…. Elegant design requires us to think about a theory of graphics, not charts.

We should think of chart names only as a shorthand for what they do. To broaden our ability to represent comparisons and insights into data, we should instead consider their representation as types of measurement: length along a common baseline, for example, or encoding data as color to create Gestalt groupings.

In Leland Wilkinson’s influential work, he develops a grammar of graphics. That grammar respects a fundamental limitation, a difference from pictures and other visual arts:

We have only a few rules and tools. We cannot change the location of a point or the color of an object (assuming these are data-representing attributes) without lying about our data and violating the purpose of the statistical graphic — to represent data accurately and appropriately.

Leland categorizes his grammar:

Algebra comprises the operations that allow us to combine variables and specify dimensions of graphs. Scales involves the representation of variables on measured dimensions. Statistics covers the functions that allow graphs to change their appearance and representation schemes. Geometry covers the creation of geometric graphs from variables. Coordinates covers coordinate systems, from polar coordinates to more complex map projections and general transformations. Finally, Aesthetics covers the sensory attributes used to rep- resent graphics.

He discusses these components of graphics grammar in the context of data and its extraction into variables. He also extends the discussion with facets and guides.

How do we perceive data encoded in this grammar?

2.1.3 Perceptions of visual data encodings

We assemble mental models of grouping through differences in similarity, proximity, enclosure, size, color, shading, and hue, to name a few. In figure 20, for example, we recognize dataset three as having a grouped linear relationship with one outlier based on proximity. Using shading, for example, we can separate groups of data. In the left panel of figure 24, we naturally see two groups, one gray, and the other black, which has an outlier. We could even enclose the outlier to further call attention to it, as shown on the right panel.

Figure 24: We can use preattentive attributes to separate data categorically and call attention to particular aspects of that data.

Several authors²² provide in-depth reviews of these ideas. We can, and should, use these ideas to assist us in understanding and communicating data through graphical displays.

Graphical interpretation, however, comes with its own limitations. Our accuracy in estimating the quantities represented in visual encoding depends on the geometries used for encoding. In other words, it can be easy for us, and less familiar readers, to misinterpret a graph. Consider the example in Figure 25 where the slope of the trend changes rapidly. Considering the left panel alone, it may seem deviations from the fitted line decrease as x increases. But the residuals encoded in the right panel show no difference.

Figure 25: Without careful inspection, it may seem that deviations from the fitted line decrease as x increases. The plot of residuals, however, shows the reverse is true.

The misperception arises if we mistakenly compare the minimal distance from each point to the fitted line instead of comparing the vertical distance to the fitted line. Cleveland (1985) has thoroughly reviewed our perceptions when decoding quantities in two or more curves, color encoding (hues, saturations, and lightnesses for both categorical and quantitative variables), texture symbols, use of visual reference grids, correlation between two variables, and position along a common scale. Empirical studies by Cleveland and McGill (1984) and Heer and Bostock (2010) have quantified our accuracy and uncertainty when judging quantity in a variety of encodings.

The broader point is to become aware of issues in perception and consider multiple representations to overcome them. Several references mentioned in the literature review delve into visual perception and best practices for choosing appropriate visualizations. Koponen and Hildén (2019), for example, usefully arranges data types within visual variables and orders them by our accuracy in decoding, shown in figure 26:

Figure 26: Visual variables, organized by how well they are suited for representing data measured on each type of scale.

Placing encodings in the context of chart types, figure 27, we decode them from more to less accurate, position encoding along common scales (e.g., bar charts, scatter plots), length encodings (e.g., stacked bars), angles (e.g., pie charts), circular areas (e.g., bubble charts), luminance, and color (Munzner 2014):

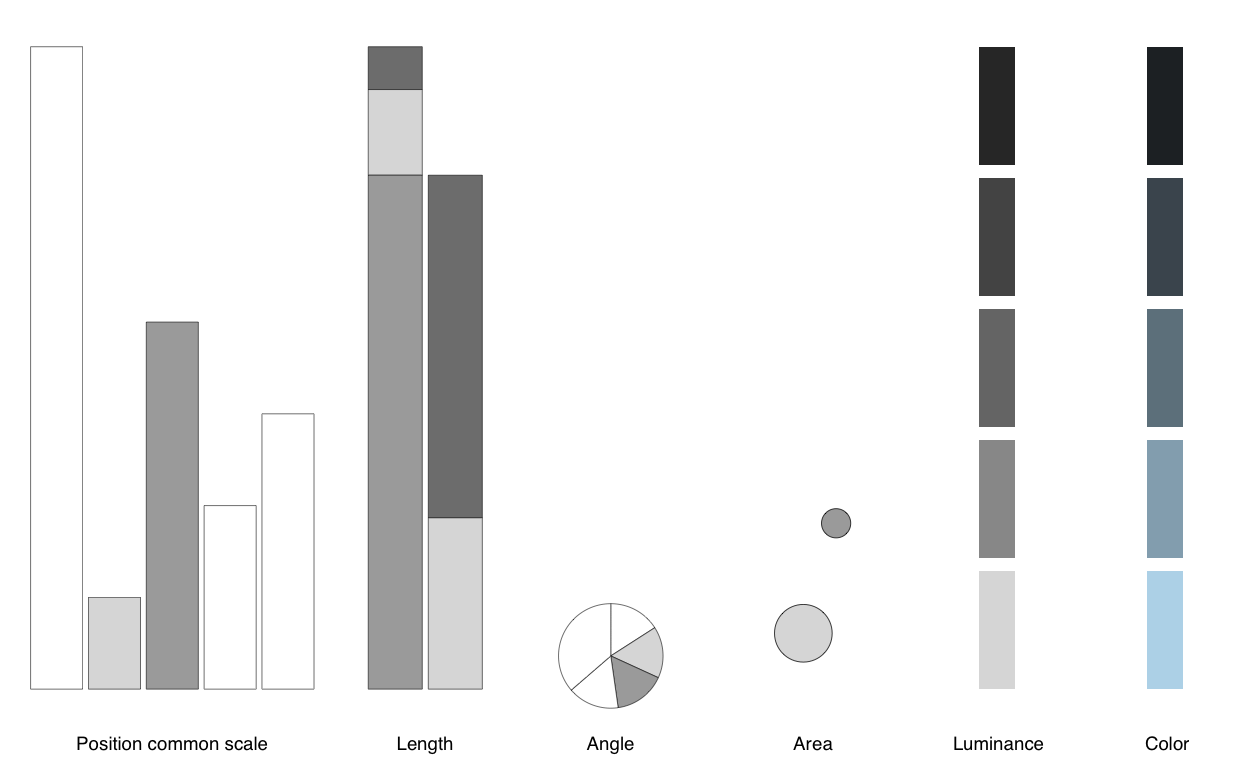
Figure 27: We gage position along a common scale more accurately than length, which we gauge more accurately than angle or area. Luminance or color are typically reserved for encoding quantities in a third dimension.

A thorough visual analysis may require multiple graphical representations of the data, and each require inspection to be sure our interpretation is correct.

2.1.3.1 Color

As mentioned, We can encode data using color spaces, which are mathematical models. The common color model RGB has three dimensions — red, green, and blue, each having a value between 0 and 255 (\(2^8\)) — where those hues are mixed to produce a specific color.

Notice the hue, chroma, and luminance of this colorspace,

seems to have uneven distances and brightness along wavelength.

Let’s consider how we might, as illustrated below, map data to these characteristics of color.

Luminance is the measured amount of light coming from some region of space. Brightness is the perceived amount of light coming from that region of space. Perceived brightness is a very nonlinear function of the amount of light emitted. That function follows the power law:

\[\begin{equation} \begin{split} \textrm{perceived brightness} = \textrm{luminance}^n \end{split} \end{equation}\]

where the value of \(n\) depends on the size of the patch of light. Colin Ware(Ware 2020) reports that, for circular patches of light subtending 5 degrees of visual angle, \(n\) is 0.333, whereas for point sources of light \(n\) is close to 0.5. Let’s think about this graphically. Visual perception of an arithmetical progression depends upon a physical geometric progression (Albers 2006). In a simplification shown in figure 28, this means: if the first 2 steps measure 1 and 2 units in rise, then step 3 is not only 1 unit more (that, is, 3 in an arithmetical proportion), but is twice as much (that is, 4 in a geometric proportion. The successive steps then measure 8, 16, 32, 64 units.

Figure 28: As Albers illustrates, Weber’s law, applied to creating color steps we perceive as evenly spaced requires we convert from an arithmetical progress to a geometric progression.

Color intervals are the distance in light intensity between one color and another, analogous to musical intervals (the relationship between notes of different pitches).

Uneven wavelengths between what we perceive as colors, as we saw in the RGB color space, results in, for example, almost identical hues of green across a range of its values while our perception of blues change more rapidly across the same change in values. We also perceive a lot of variation in the lightness of the colors here, with the cyan colors in the middle looking brighter than the blue colors.

The problem exists in each channel or attribute of color. Let’s consider examples by comparing the hue, saturation, and luminance of two blocks. Do we perceive these rectangles as having the same luminance or brightness?

Do we perceive these as having the same saturation?

Do we perceive these as having equal distance between hues?

There’s a solution, however. Other color spaces show changes in color we perceive as uniform. Humans compute color signals from our retina cones via an opponent process model, which makes it impossible to see reddish-green or yellowish-blue colors. The International Commission on Illumination (CIE) studied human perception and re-mapped color into a space where we perceive color changes uniformly. Their CIELuv color model has two dimensions — u and v — that represent color scales from red to green and yellow to blue.

More modern color spaces improve upon CIELuv by mapping colors as perceived into the familiar and intuitive Hue-Chroma-Luminance²³ dimensions. Several modern color spaces, along with modification to accommodate colorblindness, are explained in the expansive Koponen and Hildén (2019). In contrast with the perceptual change shown with an RGB colorspace above, the change in value shown below of our green-to-blue hues in 10 equal steps using the HCL model are now perceptually uniform.

For implementations of perceptually uniform color spaces in R, see Spencer (2020) and Zeileis, Hornik, and Murrell (2009). Using the perceptually uniform colorspace HSLuv, let’s explore the above hue changes, across various saturation and luminance:

With categorical data, we do not want one color value to appear brighter than another. Instead, we want to choose colors that both separate categories while holding their brightness level equal.

When mapping data to color channels — hue, saturation, or lightness — use a perceptually uniform colorspace.

2.1.3.2 Relativity of color

Notice, by the way, that each of the above 10 equal blocks from green to blue appear to show a gradient in hue. We also see this for each step in luminance (but not across blocks of saturation) in our HSLuv comparisons. That isn’t the case, the hue is uniform within each block or step. Our eyes, however, perceive a gradient because the adjacent values create an edge contrast. Humans have evolved to see edge contrasts, as in figure 29.

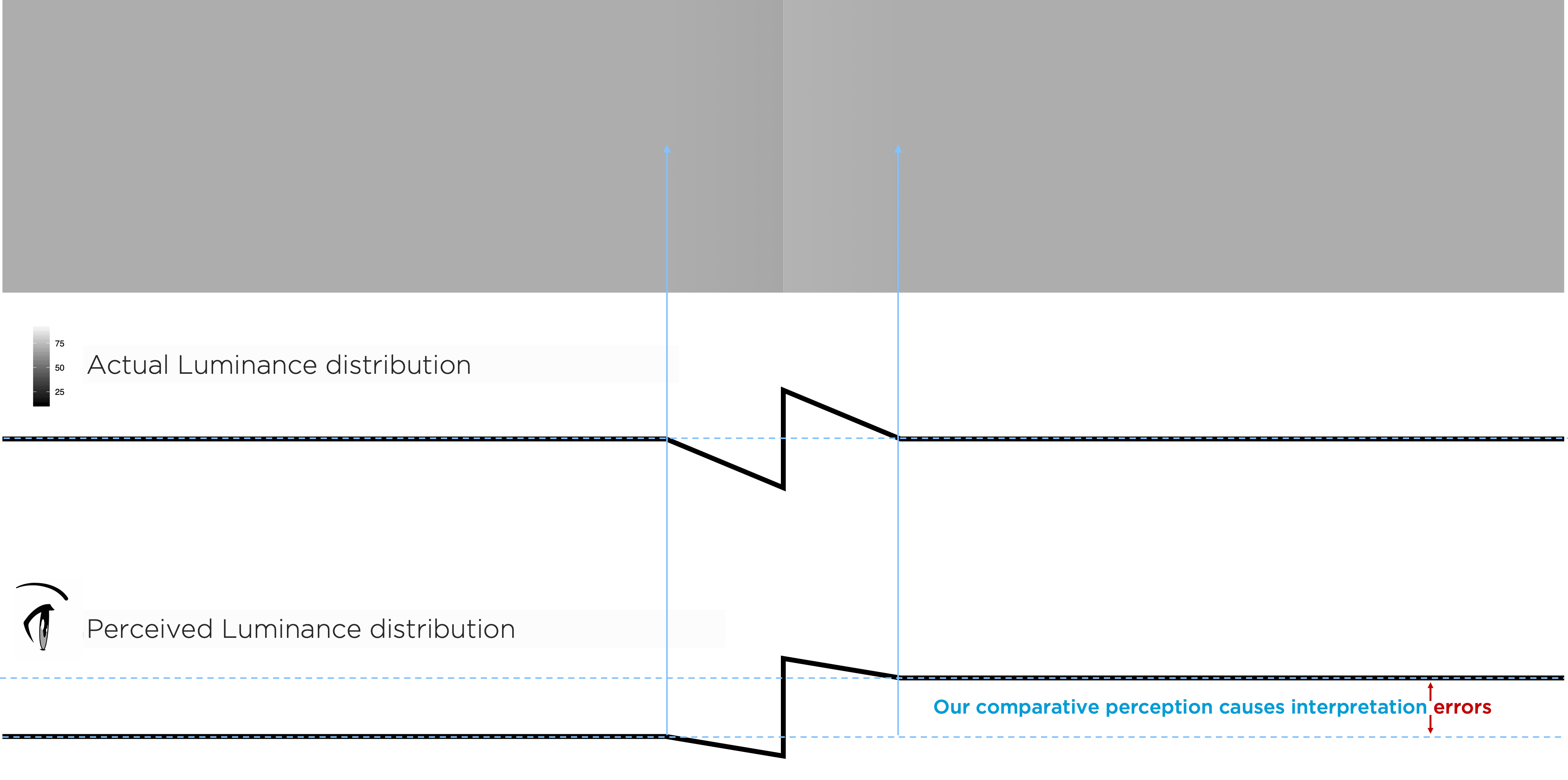
Figure 29: We see comparative — not absolute — luminance value. Adjacent data encoded by color may cause us to misperceive the value we’re inspecting.

We see comparative — not absolute — luminance value. The edge between the left and right gray rectangles in figure 29, created by a luminance adjustment tricks us into seeing each rectangle as uniform and differing in shade, though the outer portions of each have the same luminance. Need proof? Cover the edge portion between them!

Similarly, our comparative perception has implications for how to accurately represent data using luminance. Background or adjacent luminance — or hue or saturation — can influence how our audience perceives our data’s encoded luminance value. The small rectangles in the top row of figure 30 all have the same luminance, though they appear to change. This misperception is due to the background gradient.

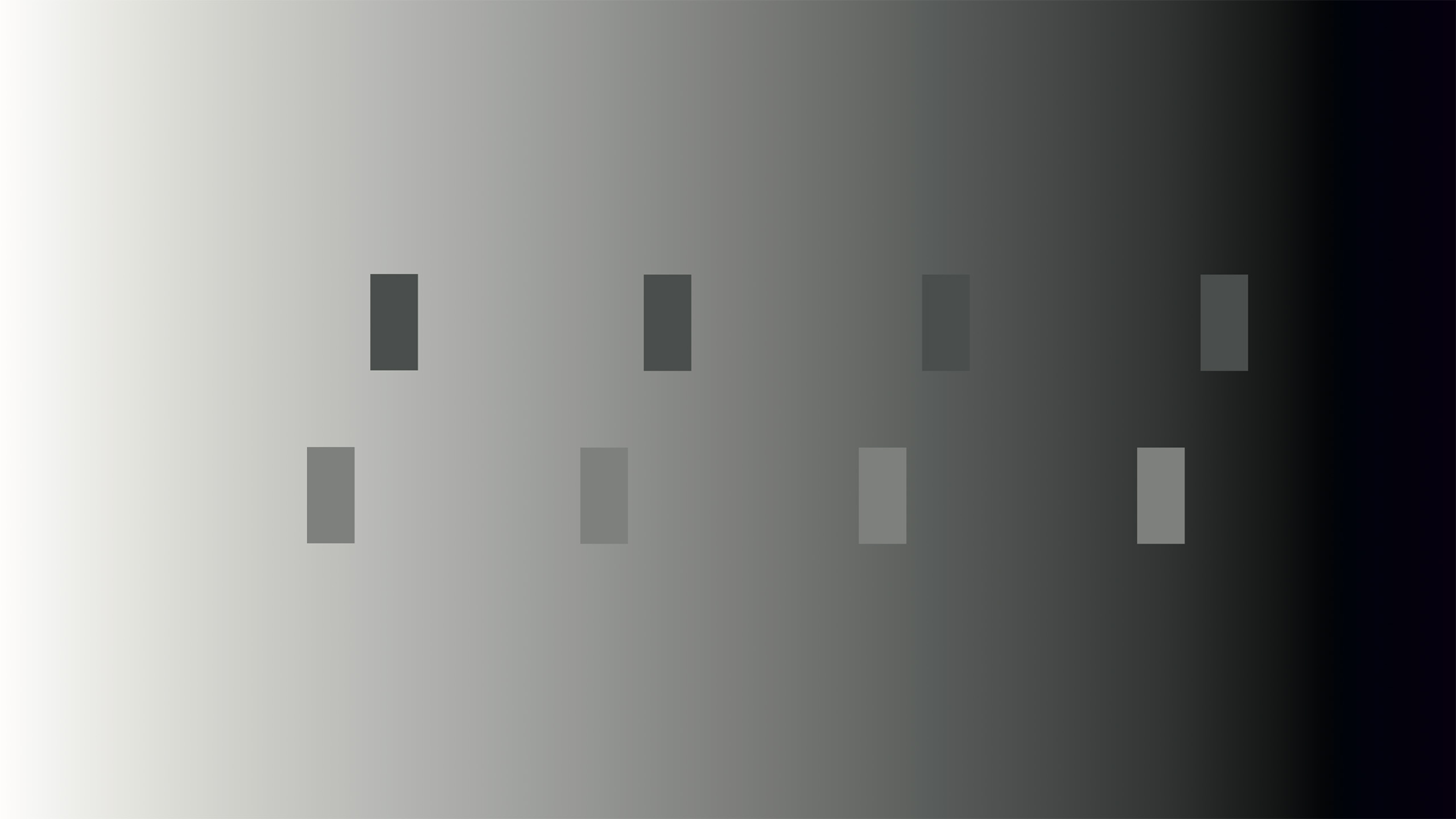
Figure 30: Background information causes us to misperceive that each row of small rectangles are encoded with identical luminance values.

One color can interact to appear as two. The inner blocks on the left are the same color, and the two inner blocks on the right are the same, but different background colors change our perception:

Two different colors can interact to appear as one. In this case, the background colors change our perceptions of the two different inner blocks such that they appear the same:

And contrasting hues with similar luminance can create vibrating boundaries:

These examples were adapted from those in Albers (2006), which discusses yet more ways the relativity of color can mislead us.

Exercise 21 Locate two or three graphics on the internet, each with different types of data-ink encodings you believe are well-designed. Be adventurous. Describe those encodings without using names of charts.

Exercise 22 Locate two graphics, each with different types of data-ink encodings you believe are problematic. Describe the encodings, what makes them problematic, and suggest a more appropriate encoding.

Exercise 23 Explain how you might use the apparent problem of vibrating boundaries to help an audience. Hint: think about why we use gestalt principles.

2.1.3.3 Special difficulties decoding color

Accounting for the reletive nature of color is already challenging. To make our work more difficult, individuals experience color differently. Some individuals, for example, have difficulties differentiation hues like between red and green.

…

2.1.4 Maximize information in visual displays

Maximize the information in visual displays within reason. Edward R. Tufte (2001a) measures this as the data-ink ratio:

\[\begin{equation} \begin{split} \textrm{data-ink ratio} =\; &\frac{\textrm{data-ink}}{\textrm{total ink used to print the graphic}} \\ \\ =\; &\textrm{proportion of a graphic's ink devoted to the} \\ &\textrm{ non-redundant display of data-information}\\ \\ =\; &1.0 - \textrm{proportion of a graphic that can be} \\ &\textrm{erased without loss of data-information} \\ \\ \end{split} \end{equation}\]

That means identifying and removing non-data ink. And identifying and removing redundant data-ink. Both within reason. Just how much requires experimentation, which is arguably the most valuable lesson²⁴ from Tufte’s classic book, The Visual Display of Quantitative Information. In it, he systematically redesigns a series of graphics, at each step considering what helps and what may not. Tufte, of course, offers his own view of which versions are an improvement. His views are that of a designer and statistician, based on his experience and theory of graphic design.

Some of his approaches have also been subject to experiments (Anderson et al. 2011), which we should consider within the context and limitations of those experiments. More generally, for any important data graphic for which we do not have reliable information on its interpretability, we should perform tests on those with a similar background to our intended audiences.

Let’s reconsider the example figure from Knaflic:

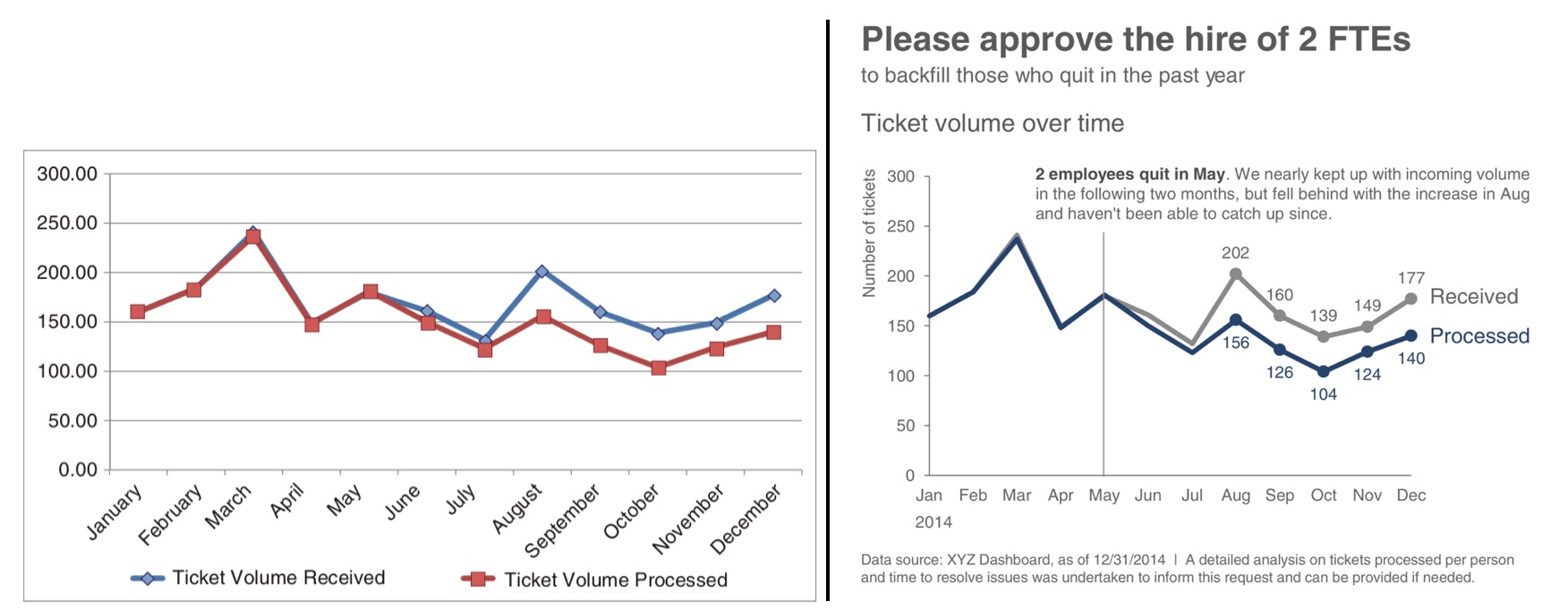
Figure 31: Knaflic systematically changes a graphic, beginning with the original, default graph on the left, and finishing with the graphic on the right.

Compare Knaflic’s before-and-after example.

Exercise 24 Try to articulate all differences. Consider whether her changes follow Tufte’s principles, and whether each of her changes would improve her audience’s understanding of the intended narrative and supporting evidence.

For the next example, revisiting the Dodgers, consider the following example analysis related to understanding game attendance as a function of fan preferences for game outcome certainty, since maximizing attendance is a marketing objective:

Example 3 To help us understand game attendance as a function of fan preference for certainty or uncertainty of the game outcome, we created a model. It included variables like day of the week, time of day, and the team’s cumulative fraction of wins. We believe that some uncertainty helps attract people to the game. But how much? It also seems reasonable to believe that the function is non-linear: a change in probability of a win from 0 percent to 1 percent may well attract fewer fans than if from 49 percent to 50 percent. Thus, we modelled the marginal effect of wins as quadratic. Our overall model, then, can be described as:

\[\textrm{Normal}(\theta, \sigma)\]

for game \(i\), where \(\theta\) represents the mean of attendance, \(\sigma\) the variation in attendance, and \(\theta\) itself decomposed:

\[\begin{equation} \begin{split} \theta_i \sim &\alpha_{1[i]} \cdot \textrm{day}_i + \alpha_{2[i]} \cdot \textrm{time}_i + \\ &\beta_{1[i]} \cdot \frac{\sum{\textrm{wins}_i}}{\sum{\textrm{games}_i}} + \beta_{2[i]} \cdot p(\textrm{win}_i) + \beta_{3[i]} \cdot p(\textrm{win}_i)^2 \end{split} \end{equation}\]

With posterior estimates from the model, we calculated the partial derivative of estimates of win uncertainty (\(\beta_2\) and \(\beta_3\)) to find a maximum:

\[\textrm{Maximum} = \frac{-\beta_2}{2 \cdot \beta_3 }\]

For the analysis, we used betting market odds as a proxy for fans’ estimation of their team’s chances of winning. The betting company Pinnacle made these data available for the 2016 season, which we combined with game attendance and outcome data from Retrosheets.

The analysis included the exploratory graphic on the left, using default graphic settings, in figure 32, and the communicated graphic on the right.

Figure 32: An exploratory graphic using R / ggplot default settings on the left, and corresponding presentation graphic on the right.

Exercise 25 Try to articulate all differences between the exploratory and communicated graphic. Consider whether the changes follow Tufte’s principles, if so, which, and whether each of the changes would improve the marketing audience’s understanding of the intended narrative and supporting evidence. Can you imagine other approaches?

2.2 Visually encoding data, common and xenographic

2.2.1 Encoding data-ink, common graphics

Resources abound for encoding and coding common graphics. In an award-winning graphic form, Holtz and Healy (2018) provides taxonomies for common graphics, and an analysis of basic charts. See also, (Healy 2018b); (Knaflic 2015); (R. L. Harris 1999); (Cleveland 1993); (Cleveland 1985). Again consulting the Data Visualization Handbook will explain common statistical graphics, including bar charts, dot plots, line charts and their variants, like slopegraphs, streamgraphs, bumps charts, cycle plots, sparklines, pie and donut charts, scatterplots (scatter or x-y, strip plot, beeswarm plot), bubble charts, heatmaps, box plots, violin plots, and many more.

We should not try to memorize each type. Instead, we should understand how they work using the language and ideas from section ??. Apply the the advice about studying metaphor and rhetorical figures (section ??) when constructing graphics, too:

Seeing just a few examples invites direct imitation of them, which tends to be clumsy. Immersion in many examples allows them to do their work by way of a subtler process of influence, with a gentler and happier effect on the resulting style.

Of note, the difference between common graphics and what has been called xenographics is somewhat arbitrary. The more important point is not the name we use — chart names are just short-hand to convey instances of graphics or look them up — but that we anticipate what encodings our audience already understands how to decode and what encodings our audience needs explanation on how to decode.

2.2.2 Layers and separation

Graphics, including data encodings, are created in layers: each marking is closer to our eyes than the previous marking. The implications are several. First, when the correct attributes of markings are used, we can perceive one marking closer than another. In the left graphic, for example, we perceive the orange circle behind the blue circle, while in the right graphic, we perceive the blue circle behind the orange circle:

These particular effects are created in code, simply by our code order for the markings, overlapping the markings, and choosing fill colors to distinguish the two shapes. We can create the same perception in other ways, too.

Samara (2014) describes these design choices as creating a sense of near and far. We may create a sense of depth, of foreground and background, using any of size, overlapping the forms or encodings, the encodings relative values (lightness, opacity). Samara (2014) writes, “the seeming nearness or distance of each form will also contribute to the viewer’s sense of its importance and, therefore, its meaning relative to other forms presented within the same space.” Ultimately we are trying to achieve a visual hierarchy for the audience to understand at each level.

When designing graphics, and especially when comparing encodings or annotating them, we must perceptually layer and separate types of information or encodings. As Edward R. Tufte (1990b) explains, “visually stratifying various aspects of the data” aides readability. By layering or stratifying, we mean placing one type of information over the top of a second type of information. The grammar of graphics, discussed earlier, enables implementations of such a layering. To visually separate the layered information, we can assign, say, a hue or luminance, for a particular layer. Many of the graphics discussed separate types of data through layering.

2.2.3 Layering and opacity

Opacity / transparency provide another attribute very useful in graphics perception. For layered data encoded in monochrome, careful use of transparency can reveal density:

The key in the above use is monochrome (a single color and shade). When we also use color, especially hue, as a channel to represent other data information, we get unintended consequences. Opacity, combined with other color attributes can change our perception of the color, creating encodings that make no sense. Let see this in action by adding opacity to our foreground / background example above, left graphic:

Notice, also, a question arises: is orange or blue in the foreground? With this combination of attributes, we lose our ability to distinguish foreground from background.

2.2.4 Encoding data-ink, xenographics

For a growing collection of interesting approaches to visualizing data in uncommon ways, consult the website Lambrechts (2020). But we have already seen a few less common data encodings. Recall, for example, instances of tracking information encoded as dots within circles in figure 9. Let’s consider a couple more. Getting back to our example Citi Bike project, we identified various data visuals used in earlier exploratory work. In that earlier study, Saldarriaga (2013), researchers visualized bike and docking station activity data in the form of heatmaps overlaying maps, and heatmaps as a grid wherein the x-axis encoded time of day, the y-axis encoded docking station names as categorical data, hue at a given time and docking station encoded the imbalance between incoming and outgoing bikes, and a luminosity gradient at the same location encoded activity level, as shown in figure 33.

Figure 33: Researchers visualized bike and docking station activity data in the form of heatmaps overlaying maps, and heatmaps as a grid wherein the x-axis encoded time of day, the y-axis encoded docking station names as categorical data, hue at a given time and docking station encoded the imbalance between incoming and outgoing bikes, and luminocity at the same location encoded activity level.

The more interesting aspect of this graphic is that, as explained in its legend, the dual, diverging hue, luminance encoding enables markings to disappear if either a) incoming and outgoing activity is balanced or b) the activity level is very low. The limitations of the overall encoding, however, include an unfamiliar listing of docking stations by name on the y-axis. As we proposed in the memo, example 1, let’s try encoding these variables differently. Let’s try addressing the admitted challenge of encoding geographic location with time in a way that allows further, meaningful encodings. We will do this in stages. First, we consider activity level, which we naturally think of as a daily pattern. Other graphics, Armstrong and Bremer (2017) and Bremer (2017), have explored daily patterns of activity, and encode that activity level using polar coordinates. We borrow from that work, encoding bike activity level the way we think about time — circular, think of a 24-hour clock. Our first graphic is in figure 34. We read the graphic as reflecting activity level over time, which is encoded circular, with midnight at the top, 6am to the right, noon at the bottom, 18 hours (6pm) to the left. To help visualize time of day, we label sunrise and sunset, and shade areas before and after sunrise as dark and light.

Figure 34: This graphic encodes bike activity levels throughout a 24-hour day, where time is encoded as polar coordinates.

As did Nadieh, we encode an average activity level along the black line, activity level at a given time as the distance from that average. And the color within that distance from average activity level encodes the quantiles (think boxplot) of activity. As with encoding average activity level, we annotate with reference activity levels: 5, 20, and 35 rides per minute. What is remarkable is the observed magnitude of change from average (black circle) ride rates that exist throughout the day, which reflects this rebalancing problem. Minutes in only light blue show when 50 percent of the ride rates exist. Minutes that include dark blue show when the highest (outside black circle) or lowest (inside black circle) rate of rides happen. Finally, the remaining minutes with medium blue show when the rest of the rates of rides occur.

We now address the limitation of the prior work. In this regard, we can learn from the famous graphic by Minard of Napoleon’s march, see figure 35.

Figure 35: Minard’s Napoleon graphic redrawn and translated into English.

In Minard’s graphic, as Tufte explains, he overlays the path of Napoleon’s march onto a map in the form of a ribbon.²⁵ While the middle of that ribbon may accurately reflect geographic location, the width of that ribbon does not. Instead, the width of the ribbon encodes the number of solders at that location, wherein time is also encoded as coinciding with longitude. That encoding gives a sense of where the solders were at a given time, while also encoding number of solders. We try a similar approach with Citi Bike, shown in figure 36. We place each docking station the a black dot (\(\cdot\)) overlaying a geographic map of New York City. At each station, we encode using color an empty or full station as a line segment ( | ) starting at the station dot and extending towards time of day, the length of a unit circle. The line segments are partly transparent so that an individual empty or full station won’t stand out, but repeated problems at that time of day over the three weeks of the data (January 2019) would be more vivid and noticeable. Finally, we annotate the graphic with a narrative and a key that explains these encodings, along with encoding the general activity levels of the graphic in figure 34.

Figure 36: The visualization — a xenographic — invites riders to explore bike and docking station availability for encouraging re-distribution for the NYC bike share. The data on trips and station availability are encoded in seven dimensions: space, time, bike and dock availability, rate of new rides per minute, and whether unavailability at a given time of day occurred multiple times. I used the metaphor of unavailability as dandelions among flowers that riders travel through each spring, weeds that need fixing and a request: by riding against the flow—redistributing bikes—those riders are helping us all.

The infographic adds, as its title, a call to action: ride against the flow (Spencer 2019a, longlisted Kantar Information is Beautiful Awards). When encoding custom graphics, basic math can come in handy. The encodings (colored line segments) for empty and full docking stations at each station were created by mapping the hour of a day to the angle in degrees/radians of a unit circle, and calculating the end of the line segments as an offset from the docking station geolocation using basic trigonometry,

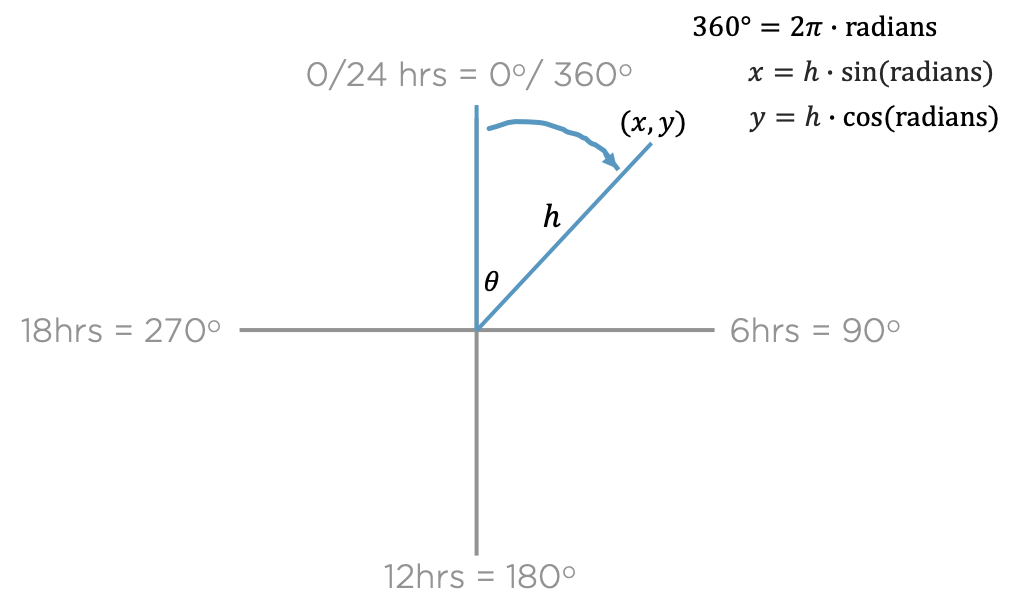
2.3 Encoding uncertainty, estimates, and forecasts

2.3.1 Motivation to communicate uncertainty

Most authors do not convey uncertainty in their communications, despite its importance (Hullman 2020). Yet good decisions rely on knowledge of uncertainty (B. Fischhoff and Davis 2014); (Baruch Fischhoff 2012). Scientists are often hesitant to share their uncertainty with decision-makers who need to know it. With an understanding of the reasons for their reluctance, decision-makers can create the conditions needed to facilitate better communication. The failure to express uncertainty has a negative value. Communicating knowledge can worsen results if it induces unwarranted confidence or is so hesitant that other, overstated claims push it aside. Quantifying uncertainties aids verbal expression.

If we perceive the concern: people will misinterpret quantities of uncertainty, inferring more precision than intended. We might respond: Most people like getting quantitative information on uncertainty, from them can get the main message, and without them are more likely to misinterpret verbal expressions of uncertainty. Posing clear questions guide understanding. Concern: people cannot use probabilities. Response: laypeople can provide high-quality probability judgments, if they are asked clear questions and given the chance to reflect on them. Communicating uncertainty protects credibility. Concern: credible intervals may be used unfairly in performance evaluations. Response: probability judgments give us more accuracy about the information; i.e., won’t be too confident or lack enough confidence.

2.3.2 Research in uncertainty expression

Hullman (2019) provides a short overview of some ways we can represent uncertainty in common data visualizations, along with pros and cons of each. Recent ideas include hypothetical outcome plots (Kale et al. 2018), quantile dotplots (Fernandes et al. 2018) and (Kay et al. 2016), like this,

where the reader can count or estimate the relative frequency occurring at at given measurement, and compare the numbers above or below some threshold. Or values coded with hue and luminosity to create a value-suppressing uncertainty palette (Correll, Moritz, and Heer 2018),

and gradient and violin plots (Correll and Gleicher 2014), as used below in, for example, figure 38.

Missing data create another form of uncertainty, and are common in data analytics projects. The worst approach, usually, is to delete those observations, see (Little and Rubin 2019) and (Baguley and Andrews 2016). Instead, we should think carefully about an appropriate way to represent our uncertainty of those values, usually through multiple imputation. This approach means we treat each missing value as an estimated distribution of possible values. We also need to communicate about those missing values. There are other approaches (Song and Szafir 2018) for visualizing missing data.

Data are part of our models; understanding what is not there is important.

2.3.3 Estimations and predictions from models

To persuasively communicate estimates and predictions, we must understand our models. Our goal in modeling is most typically to understand real processes and their outcomes, to understand what has happened, why, and to consider what may transpire.

Data represent events, outcomes of processes. Let’s call the data observed variables. Typically, we do not know enough about the process to be certain about which outcome will be next: if we did, we wouldn’t need to model it!

But with some knowledge of the process — even before knowing the observed variables — we have an idea of its possible outcomes and probability of each outcome. This knowledge, of course, comes from some kind of earlier (prior) data, perhaps from various sources.

We’ve mentioned that visualization is a form of mental modeling of the data. Visual displays enable us to find relationships between the variables of interest. But not all relations lend themselves to the displays at our disposal. This is especially true as the quantity and type of variables grow.

2.3.3.1 Conceptualizing models

Complementary to visual analyses, we code models to identify, describe, and explain relationships. We have already used a basic regression model earlier when exploring Anscombe’s Quartet. That linear regression could be coded in R as simply lm(y ~ x). But mathematical notation can give us a more informative, equivalent description. Here, that might be²⁶,

\[\begin{equation} \begin{split} y &\sim \textrm{Normal}(\mu, \sigma) \\ \mu &= \alpha + \beta \cdot x \\ \alpha &\sim \textrm{Uniform}(-\infty, \infty) \\ \beta &\sim \textrm{Uniform}(-\infty, \infty) \\ \sigma &\sim \textrm{Uniform}(0, \infty) \end{split} \end{equation}\]

Considering a second example, if we are given a coin to flip, our earlier experiences with such objects and physical laws suggest that when tossed into the air, the coin would come to rest in one of two outcomes: either heads or tails facing up. And we are pretty sure, but not certain, that heads would occur around 50 percent of the time. The exact percentage may be higher or lower, depending on how the coin was made and is flipped. We also know that some coins are made to appear as a “fair” coin but would have a different probability for each of the two outcomes. Its purpose is to surprise: a magic trick! So let’s represent our understanding of these possibilities as an unobserved variable called \(\theta\). \(\theta\) is distributed according to three, unequal possibilities: The coin is balanced, heads-biased, or tails-biased.

2.3.3.2 Visually communicating models

Then, we can represent our prior understanding of the probability of heads as distributed, say, \(\textrm{Beta}(\theta \mid \alpha, \beta)\) where \(\theta\) is the probability, and \(\alpha\) and \(\beta\) are shape parameters, and the observed data distributed \(\textrm{Binomial}(\textrm{heads} \mid \textrm{flips}, \theta)\). If we were very confident that the coin was fair, we could keep the prior distribution narrowly near a half, but in this example we will leave extra uncertainty for the possibility of a trick coin, say, \(\alpha = \beta = 10\), as shown in the left panel of figure 37. For 8 heads in 10 flips, our model distribution with this data are shown in the middle panel of Figure 37.

Figure 37: Our prior knowledge of coins and the observed data combine to inform our new understanding of, and uncertainty in, the probability of heads with this coin.

When our model combines the two sources of knowledge together, shown on the right panel of figure 37, we get our updated information on, and uncertainty of, what the underlying probability of heads may be for this coin. Such distributions most fully represent the information we have about, and should be considered when describing our modeling. With the distributions in pocket, of course, we can summarize them in whatever way makes sense to the questions we are trying to answer and for the audience we intend to persuade. figure 38 provides one alternative for expressing our knowledge and uncertainty.

Figure 38: We can think of this summary as a top-down perspective on the above distributions. We lose some information because it is difficult to capture differences in plausibility through transparency settings alone, but the approach still conveys uncertainty, and the skewed distribution of the likelihood.

The above is a more intuitive representation of the variation than in table 4. Tables may, however, complement the information in a graph display.

Table 4: Tables do not offer the same ability to quickly understand uncertainty or compare differences between states of information. But they can complement, shape, and provide numerical precision to what we perceive in the graphic.

	Range of possible probabilities of heads
Knowledge	Min	25th	50th	75th	Max
Prior	0.12	0.43	0.50	0.58	0.88
Likelihood	0.20	0.67	0.76	0.84	0.99
Posterior	0.23	0.54	0.60	0.66	0.91

Modeling is usually, of course, more complex than coin flipping and can be a vast, complex subject. That does not mean it cannot be visualized and explained persuasively. Much can be learned about how to explain what we are doing by reviewing well-written introductions on the subject of whatever types of models we use. There are several references — for example, (McElreath 2020) and (Stan Development Team 2019) — that thoroughly introduce applied Bayesian modeling.

McElreath explains what models are, and step-by-step explains various types in words, mathematically, and through corresponding code examples. These models are various: continuous outcome with one covariate, a covariate in polynomial form, multiple covariates, interactions between covariates, generalized linear models, such as when modeling binary outcomes, count outcomes, unordered and ordered categorical outcomes, multilevel covariates, covariance structures, missing data, and measurement error. Along the way, he explains their interpretations, limitations, and challenges.

2.3.3.3 Causal relationships

McElreath also introduces the importance of thinking causally when modeling. This is especially important in selecting variables. One variable may mask — confound — the relationship between two other variables. We can think about relationships and causation with a tool called a directed acyclic graph (DAG). McElreath discusses four types of confounds, and the solutions to avoid them, so that we may better understand the relationships between variables of interest. His instruction is especially helpful as it is provided an applied setting with examples. For more in-depth understanding of causation, consult Pearl (2009).

2.4 Combining data graphics in a visual narrative

Recall our first layer of messages for a graphic should be annotation of the graphic itself, as first discussed in section ??, and that we should consider data graphics as paragraphs about data and include them directly into the paragraph text, as discussed in section ??. We can broaden the concept of integrating or combining graphics and text to think about graphics as part of the overall narrative.

References: (Rendgen 2019); (Boy, Detienne, and Fekete 2015); (Hullman et al. 2013).

3 Interactive

All we’ve discussed preceding this section is a prerequisite to interactivity — whatever we mean by that — because all those concepts about communication and graphics best practices still apply. Stated differently, if you haven’t used those principles from static graphics when making an interactive graphic, adding interactivity will just be an interactive version of an ineffective graphic.

3.1 Foundations of interactive data-driven, visual design

We interact with computers, iphones, and tablets by performing actions through interfaces: commonly, a keyboard, or mouse, or trackpad, or directly on a screen. Typical actions include pointing, hovering, touching, scrolling, clicking, pressing, dragging, pinching, swiping, or other gestures:

It is worth noticing that the intuitive concept of hovering a pointer with a trackpad just requires moving on those devices, but if directly engaging with a screen, we have to touch it. And that can make an equivalent direct-touch action for hovering more challenging.

Through these actions, we interact with various graphical elements, like these:

But what are we talking about when we talk about interactive graphics? Remember the first data graphic in this text, Figure 1 showing the baseball fields and fences? It was used to explain the importance of context? What you can’t really tell by just inspecting the graphic is that it consists of two separate graphics, one above the other. The top graphic shows the boundaries of the 30 major league baseball fields. And the bottom graphic shows the relative heights of the outfield fences for each field. Now, before interacting with it, all the 30 lines in both graphics are overlain on top of each other. We can’t really distinguish which field each line refers to, but we can get a sense of the variation and scale for both the field dimensions and the fence heights, would you agree?

But the graphic also allows us to interact with it. The graphic responds in four ways. First, it bolds or emphasizes the fence line my mouse pointer has touched. Second, it lightens or deemphasizes all the other field boundaries. Third, it shows a label or tooltip identifying the field. And I just coded an index of 1 to 30 here, but I could have gathered the field names and show that instead. As we’ll discuss soon, you can think about this as showing “details on demand.” And fourth, touching the particular link also links to the same emphasis and deemphasis in the lower graphic to show which fence height relates to the field boundary I selected or hovered over.

Interactive graphics may bring to mind graphics like our first example, Figure 1, publications like Roston and Migliozzi (2015) or Aisch and Cox (2015) or Mike Bostock, Carter, and Tse (2014), all exemplary for their audience and purpose. Notice the range of interactivity in each. We’ve already discussed the interactivity of Figure 1, simply hovering. In Roston and Migliozzi (2015), the main form of interaction is simply scrolling. The entire graphic reacts in multiple ways to the readers’ flick of the finger. We might view Aisch and Cox (2015) as requiring a bit more from its audience: clicking. And yet more is required from audiences who want to explore Mike Bostock, Carter, and Tse (2014). Along with clicking, readers click and drag sliders, enter text into text boxes, among other things. Along with these examples, Hohman et al. (2020) provides many different exemplary interactive graphics for categories of interactivity.

This text, Data in Wonderland, was created in RStudio, and we can make interactive graphics using RStudio. Is RStudio an interactive graphic?

RStudio is a web browser application with a graphical user interface. We can “interact” with it by entering text (code), clicking buttons (consider the “back”, “next”, and “zoom” buttons for a series of graphics you’ve made), etc. In response, RStudio changes the view of the data graphic we see. Is this an interactive graphic? We can make interactive graphics in Lyra2, but is Lyra2 an interactive graphic?

Lyra2 is a web browser application with a graphical user interface. We can “interact” with it by dragging and dropping, clicking buttons, similar to Tableau but free, open-source, and based on the powerful Vega / D3 javascript languages. In response, Lyra2 changes the view of the data graphic we see. Is this an interactive graphic?

Each of these examples fits how Tominski and Schumann (2020) describes interactivity — as a “human in the loop” of an iterative process of executing something in a system pursuant to some goal and evaluating what results.

The authors list, as forms of interaction with data graphics, the following possibilities:

• source code editing.
• Scripting commands.
• Graphical interfaces.
• Direct manipulation.
• And direct touch.

Let’s consider each of these.

Source code editing. An example here might be C++ and the graphics library graphics.h. On the implementation level, a visual representation is defined by source code. Only a few lines of code need to be edited to set the visualization view to where the nodes of interest are located. The altered code is compiled and run to see if the visual result is as expected. If not, the procedure is re-run until the user is satisfied. Changing code lines, re-compiling, and test-running the visualization is the least direct form of interaction, as it exhibits large conceptual, spatial, and temporal separation.

Scripting commands. R and the R package ggplot2 would be one example. Alternatively, the visualization may offer a scripting interface allowing the user to enter commands to zoom the view. Once issued, the commands take effect immediately while the visualization is running. In this scenario, no separate compilation is necessary, which reduces the temporal separation. But still the interaction is rather indirect, and several commands may be necessary before the view fits as desired.

Graphical interface. This brings to mind buttons, sliders, and text boxes. The field of view is displayed in a graphical interface alongside the visualization. Standard controls such as buttons and sliders allow the user to easily shift the view and control its zoom factor. Any changes are immediately reflected in the graphical interface and the visualization. Given the fact that the graphical interface represent the view status and at the same time serves to manipulate it, the conceptual gap is narrowed. Yet, the interaction (with the controls) and the visual feedback (in the graph visualization) are still spatially separated.

Direct manipulation. Examples of this graphical element touched by a pointer directed with a mouse or trackpad. The user zooms the view directly by drawing an elastic rectangle around the nodes to be inspected in detail. This is a rather simple press-drag-release operation when using the mouse. During the interaction, visual feedback constantly indicates the frame that will make up the new view once the mouse button is released. Any necessary fine-tuning can be done using the mouse wheel. In this scenario, the manipulation of the view takes place directly in the visualization. There is no longer a spatial separation between the interaction and the visual feedback. Or is there?

Direct touch. To obtain a yet higher degree of directness, the interaction can alternatively be carried out using touch input on the display. Think iPhones and iPads. The basic principle of sketching an elastic rectangle to specify a new view is maintained, but the action is performed using a finger directly on the display. Now, the interaction takes place exactly where the visual feedback is shown. A truly direct way of zooming in on a node-link diagram.

So to know what level of interaction seems appropriate, we should consider what? Our audience and purpose? So maybe we need to consider our audience in deciding what type of interactivity we want to provide? Before we think about audience, though, let’s briefly consider why we tend to like interactivity.

Forty years ago, Jaques Bertin explained, interactivity enables us to more quickly find relationships in the data:

A graphic is not “drawn” once and for all; it is “constructed” and reconstructed until it reveals all the relationships constituted by the interplay of the data. The best graphic operations are those carried out by the decision-maker himself (Bertin 1981).

Interesting. This sounds a lot like how we distinguished exploratory graphics from explanatory graphics doesn’t it? He seems to be talking about what we’ve described as exploratory work, for ourselves.

And in exploring what are some of the goals? We may want to mark something as interesting. We want to see different things, or different arrangement of things. Or a different representation or transformation of a thing. We want to look at more or less detail in a group of things. We want to see a thing given that some other thing happened, in other words see a set of data conditionally. Very importantly, we want to see related things, so we can compare and contrast them to provide meaning. Or maybe we want to go back to a previous data graphic. I’m sure you could list many more reasons, right?

Having started thinking about why we want interactive graphics, let’s think about how we interact, even if we’ve already discussed a few ways, and even if this seems obvious. It is helpful to list or categorize them so we have a sense of possibilities.

First off, we have common interfaces we can use to interact. We have a keyboard. We have a mouse. We have a trackpad. And with some devices, we can touch the screen directly. Now there are other ways, like virtual reality, but for this discussion we’ll stick with the common ways I’ve just listed.

Now we can interact with graphical systems in through actions you find common, either with our hands directly on the screen, or with a pointer we direct with a mouse or trackpad. Let me say something that’s a bit special about pointing or hovering. That’s something we can easily do with the trackpad but can’t when using our hands directly, right? So some of these actions are specific to what interface we choose. Of course, we’ve already seen several of these in action with our examples. Scrolling and Clicking. We can also interact by only a part of the click action. It actually involves several sub actions. We can press and hold to perform a separate action from the immediate release, for example. And we can drag things, swipe. Pinch or spread, rotate, and use various other gestures. And we shouldn’t be surprised when new things become available to us, right? So the systems we use listens for these actions and links them to various graphical elements. Or we do that by coding the instructions to do so.

And we’ve already seen various ways that actions can trigger events. In the rent or buy article example, again, it linked our actions for entering text and our actions for pressing and dragging a slider to other graphical elements, right? And in the yield curve article, it linked clicking on the back and next buttons to advancing animations and next graphics views. The first example with the baseball fields more directly linked our actions to the graphical elements, right?

So we can either use widgets or link actions directly to data elements.

And when we start mixing and matching things and ideas, we have more options than we’d like to count, but we should match what we do to either our audience’s past experiences and expectations, provide descriptions and explanations for new ways we want our audience to interact, i.e., take actions to get responses, or both. Part of thinking about our audience is thinking about what tasks they may want to perform. I’ve categorized common tasks as, one, specifying a data and view. Two, manipulating that view. And three, considering the process and provenance of the data and analysis. So we can perform various tasks that relate to these things. We choose visual encodings, filter, sort, transform data. Select. Show more or less detail. Link views. Organize multiple views together. And so forth. If these are common tasks, how might we think about ordering or arranging what’s available to an audience?

Twenty-five years ago, the computer scientist Ben Shneiderman wrote an article, Shneiderman (1996), that generalized how we tend to want to interact with information. First we want an overview of the entire collection — whatever that means — then we zoom in things we are interested in, we filter out things we are not interested in, and we select particular items or groups of items to get more details when needed. Totally makes sense, right?

If we base how timely the advise still is, other research continues to cite Ben’s work and we see this mantra all over the place. By the way, Ben focuses on user experience, not just data graphics. So what does it mean to have an overview of something and what does he mean by an entire collection?

Let’s pull out the Oxford English Dictionary. It’s defined in part here as “a comprehensive review of facts,” “a broad or overall view of a subject,” and “A view from above,” which sounds something like zooming out to see the whole of something, right? Before thinking about this in terms of data graphics, let’s start with something more familiar. Books.

Consider Darwin’s sixth edition — sixth edition — of The Origin of Species, and the first page of the table of contents:

Is the table of contents an overview of the book? Can a book’s table of contents be an overview? Is an overview summarizing? Showing all of something? Both? Neither? Why or why not?

What about a book’s introduction? Review the introduction from Darwin’s book:

In it, he tells his readers what each chapter is about. Is this an overview? Why or why not? Or should we show every word in his book? A company did just that. The company Fathom created a data graphic of all the words in his sixth edition, and color coded where each word first appeared, which addition Darwin first published that word or sentence (Fry, n.d.). Please review their original, but here’s a screenshot:

It’s also an interactive, by the way, so I’ll invite you to click and check it out before continuing. The encodings show that the entire chapter VII did not appear until the sixth edition²⁷. So is this an overview? Or was Darwin’s table of contents an overview? Neither? Or were both? Let’s listen to what another researcher in visualization says.

Tamara Munzner, a professor of computer science visualization researcher, in Munzner (2014) explained:

“A vis idiom that provides an overview is intended to give the user a broad awareness of the entire information space. A common goal in overview design is to show all items in the dataset simultaneously, without any need for navigation to pan or scroll. Overviews help the user find regions where further investigation in more detail might be productive.”

Does this help explain the mantra in Shneiderman (1996), “Overview first, zoom and filter, then details-on-demand”? Munzner thinks the intention is to show the “entire information space”. “Show all items in the dataset simultaneously.” What do you think?

It’s pretty easy to show lots of observations of a few variables at the same time. But what about when we have many variables? How can we accomplish this? What use would it be?

Remember all the exploratory work we considered for the Citi Bike example, looking at different partial views of the data? And from that work, we created Spencer (2019a) ? This graphic shows all station locations, each station’s id, latitude and longitude, it shows where that is in relation to geographic boundaries, it shows, when a station is empty or full, which we calculated, and shows the time of day when that event happened. It shows overall activity level throughout the 24 hour period, and it shows the time of sunrise and sunset. But, if you recall (or go back and review now), even this version of the data did not show all the information. We had lots more data variables than that that we did not show here. We had available, at any given moment, the number of bikes and number of available spaces, and we had data on the sex of each rider and birth year, we had weather information we could join with each ride, that include time, temperature, wind speed and direction, humidity, rain or sunshine or cloudy, and more. We found, and decided that subway entrance and exit locations seemed relevant, and local traffic conditions.

Given all these data we did not show, is Spencer (2019a) what Munzner would call an overview?

A couple more authors have investigated what visualization designers mean when they use the term overview. As published in Hornbæk and Hertzum (2011), the authors gathered, from thousands of journal articles and conference proceedings, descriptions that use “overview” and categorized the concepts that the term was meant to convey. From that study, the authors conclude that what constitutes an “overview of an information space” depends:

What constitutes an overview of an information space may differ depending on whether the task is a monitoring task, a navigation task, a planning task, or the user has some other focus.

It depends on what kind of task is being performed, and what focus the user has in working with the graphic. Ah, that makes more sense! The authors also modeled a working definition of overview from all the researched uses. Here it is:

Figure 39: Empirically studied uses of the term overview in the context of interactive graphics.

While it’s shown as a schematic, we can read it as a definition with parts. An overview is an awareness of the content, the structure, and the changes, of an information space that is acquired by pre-attentive cues, either when initiating or through a given task. An overview is useful for monitoring, navigating, exploring, understanding, planning. To be useful it should have good performance. And we create such overviews using either static or dynamic visuals that shrink or zoom out to see the entire information space we’re interested in.

So if we’re interested in measures of a single variable, we show all measurements together. Or maybe measures for two attributes of observations, we show all those. And if you think about it, we reason about relationships between things. But it becomes increasingly difficult and complex to reason about many interactions of things at once. So maybe our overview shows all measurements of attributes related to the particular interaction or relationship for a specific task.

Now that we’re starting to think about an overview first, Shneiderman says we typically follow that up by zooming or filtering. Let’s go back to our example, Darwin’s book and the Fathom project.

Notice that, first, we decode all the color-coded words together. Then, we can hover over any sentence to zoom in on that sentence. The zoomed in sentence is shown as a tooltip, similar to how we commonly (though not only) show details-on-demand with interactive graphics.

As an aside, it’s important to keep in mind how our graphics are rendered. There are two ways, as raster graphics or as shapes, vector graphics. And there are trade-offs to each. If we zoom in on raster graphics, which are shapes in the form of pixels, they start looking ugly or low resolution. If we specify that our graphics render shapes as vectors, then when we zoom in, we keep high resolution. That’s a major advantage to vector graphics, and there are other advantages we won’t discuss now.

But there can be one disadvantage, too. When there are millions of shapes to be shown on a graphic, our computers get bogged down and performance of showing the shapes slows. But if we render the graphic with pixels, that isn’t an issue.

The example CitiBike graphic we just looked at has more than 100,000 shapes shown, and the file size gets a little large and it can be a little slow to show them on some devices. If there were millions, then I’d probably need to change to pixel-based shapes. For the interactive version of Spencer (2019a) that allows the reader to hover over stations for their street names and for activity levels throughout the day, for interactivity to work at all on contemporary computers, we had to rasterize the layer ²⁸ containing all the segments that indicated empty or full stations. For those familiar with Adobe’s creative suite, Illustrator works well with vector graphics, and Photoshop does the same for raster graphics.

Next, think about what actions we should consider linking or binding to zooming, filtering, and showing details-on-demand? Before concluding, let’s consider what an editor at the New York Times says.

Archie Tse, Deputy Graphics Director at The New York Times, in 2016 explained,

Readers just want to scroll. . . . If you make the reader click or do anything other than scroll, something spectacular has to happen.

he explained that they used to show lots of interactive graphics that asked the user to click, or do other things. And the Times has learned by watching readers behaviors when on their website articles that users mostly do not click, or use a drop down list or a slider, or other widget. They learned that those things tend to feel like barriers for the user to get information. And other research suggests that at least for some audiences, even adding narrative may not be enough to overcome this learned behavioral preference (Boy, Detienne, and Fekete 2015).

But if we link graphics responses to just scrolling, our users tend to like that. This works particularly well when holding a graphic in place while scrolling text beside the graphic:

Then we link changes to the graphic to locations of anchors in the scrolled text (and animate the transitions between these states). Again, he says, “Readers just want to scroll… If you make the reader click or do anything other than scroll, something spectacular has to happen.”

Reconsider the three publications cited at the beginning of this section, their specific purposes, and what each published article asked of its reader.

Very recently, the CIO of Datawrapper and former editor, also from the New York Times, weighed in (Aisch 2017). Gregor explained that we can still ask users to take actions beyond scrolling, and that things like hovering and clicking can be helpful for three reasons. It helps interested readers dig deeper into the information and details. It helps them see different views of the data. And by showing them more, it helps to build trust through transparency. Just don’t hide important information behind an interaction:

Knowing that the majority of readers doesn’t click buttons does not mean you shouldn’t use any buttons. Knowing that many many people will ignore your tooltips doesn’t mean you shouldn’t use any tooltips. All it means is that you should not hide important content behind interactions” like “mak[ing] the user click or hover to see it.

In our discussion, we have begun to consider the foundations of modern user interaction in the context of data-driven, visuals and narratives. Such interactions may trigger scrolling, some overview, zooming in or out, filtering, or showing details-on-demand, providing context to a relationship, history or context, extracting. Other helpful interactions include brushing and linking; hovering; clicking; selecting; and gestures. Part of allowing interaction results in authors having less control over the intended narrative and, thus, may think about interaction as giving the audience some level of co-creation in the narrative.

Next, we begin to consider the technologies that enable these interactions.

3.2 Technologies and tools of interactive data-driven, visual design

3.2.1 Technology stack for interaction

Interactivity is inherently technology dependent. We discuss modern approaches to interactivity as related to data-driven, visual graphics and narratives. As such, we will introduce a modern technology stack that includes html, css, svg, and javascript, within which technologies like d3.js (a javascript library) and processing operate. Most award-winning interactive graphics, especially from leading news organizations, use this stack.

But we can enable interactivity through interfaces, too, from R and Python interactive and markdown notebooks and code, to htmlwidgets, Shiny, and plotly. Then, we have drag-and-drop alternatives like Lyra2 or Tableau. While Tableau is functionally much more limited, a use-case for Tableau may be, for example, when a client has a license for it, wants basic interactivity for someone else to setup the visual with interactive options. The range of tools is becoming ever larger. More generally, knowing a range of tools will help us not only build our own interactive graphics, but will also help us work with specialists of these technologies.

3.2.1.1 Browsers

We’ve all been using a web browser many years. I remember pre-internet days, but some of you were probably born after it already existed! Common browsers today include Safari, Chrome, and Firefox.

All of these browsers work very similarly, in that they work with your operating system, whether a computer or smart phone or smart tablet or whatever, to listen for your actions within the browser window.

These are the same actions we discussed in the previous section. The browser watches for these events, and reports the events to things in the webpage you are reading.

3.2.1.2 Document Object Model

The web pages that load into your browser are typically named html files. These are just plain text files that contain lots of different kinds of code, which we will discuss in a moment. All that plain text is organized in something called a Document Object Model²⁹. That’s really just a fancy word to say what I’m minimally showing you in this small example. A Document Object Model, or DOM, consists of nested pairs of tags, and a tag is written as angle bracket pairs with the name or type of tag inside them:

All webpages have the first and last tag, above, with html inside them. All pages have a tag pair with the word head inside. And all pages have a tag pair with the word body inside. The tag pair <html></html> informs the browser, “hey I’m a web page, so you know what’s inside me.” The tag pair <body></body> are where we place content that our readers generally see, what the browser displays to them. And the tag pair <head></head> instructs the browser how to format, organize, and display the content, among other things, but the instructions inside <head> tags are not actually displayed. All these tags are part of the <html> specification. Let’s consider them more closely.

3.2.1.3 html elements

html³⁰ elements are added to the content of a page to describe its structure. An element consists of an opening tag, sometimes an attribute (like a class or style), content, and a closing tag:

In the above example, the <p></p> instructs the browser to structure the content as a paragraph. There are many pre-defined tag types and attributes, and we can define our own. Also, notice that, for closing tags, a forward slash / precedes the tag name, here p, signifying the end of that element. The attribute in this example is a css (cascading style sheet) class, which I’ve named cycling_team and defined between style tags. Finally, we place our content between the opening and closing tags, whether that content is text, like “Education First” in this example, or other things like data graphics.

Duckett (2011) is helpful for the basics of html and css, which we consider next.

3.2.1.4 Cascading style sheets — css

The dimensions of content in an html document, whose dimensions can be understood in terms of boxes surrounding that content, called the “box model” where, by default width and height attributes for an element relates to the content, and the remaining space around that content is specified by its padding, border, and margin:

Figure 40: The dimensions of styled content are measured width and height, plus sizes for padding, border, and a margin.

It is usually more convenient to size content by the size of the border box such that things inside shrink to fit, making combining components more predictable. This is achieved by adding box-sizing: border-box³¹ to css style rules.

css style rules³² Indicate how the contents of one or more elements should be displayed in the browser. Each rule has a selector and a declaration block. The selector indicates to which element(s) the rule applies. Each declaration block specifies one or more properties and corresponding values. Below, applying the class .cycling_team to a tag as an attribute,

will color the text a pink hue. css rules are specified within <style> tags:

Here, our css class sets the color of the text: Education First.

Helpful references for digging deeper into modern css include Attardi (2020); and Grant (2018). These also discuss css grid, which we consider next.

3.2.1.5 css grid

In earlier sections, we’ve talked about using grids to arrange things. Things like memos, proposals, and so forth. These grid are generally invisible but helps us organize and align information.

We can imagine using grids to create things like dashboards for data graphics, too. Fortunately, using grids in html pages has become straight-forward recently with advances in css, including css grid³³.

As an aside, the cascading part of css means that the browser applies what you write in the order we write our classes, which means that, here, if we defined multiple classes that, say, both color text, the browser uses rules to know which thing to apply. We won’t get into the details here. Let’s consider one minimal way we can specify a css grid.

Below, we define a class .gridlayout and in that specify {display: grid;} and related properties,

Then, we use our class attributes in divider tags <div></div> to format the content. The example below displays a 2 x 3 grid of cells, each with a size specified and placed in row major order. When we create classes to format specific content — like .item or .area in this example — we include formatting information in the class. Notice that .area includes grid-column and grid-row. These refer to the boundary lines around the rows and columns where we want to place our content. When we do not specify these, like in our .item class, css grid just places the content in whatever cells are available in row-major order.

We’ll come back to grids later. First, let’s discuss the last three main technologies used for document object models.

3.2.1.6 Scalable vector graphics — svg

Scalable vector graphics³⁴ — svg — are human-readable descriptions of a collection of shapes or paths that the browser can display. As we’ve discussed, enlarging vector graphics, unlike raster-based graphics, will not reduce resolution. Together these paths and shapes comprise a graphic, which we place in the html document body between <svg> and </svg> tags:

Shapes I commonly use include the circle <circle>, rectangle <rect>, text <text>, path <path>, and group <g>. By the way, we can edit vector graphic shapes using software like Adobe Illustrator or Inkscape, too.

Of note, when we code our own shapes directly, like this, our directions differ from what we may be used to with data graphics. With those, we normally think about the origin as starting towards the lower, left corner and increasing to the right and up. For svgs it’s not quite the same. Values do increase as we move to the right, but unlike with how we typically read data graphics, the origin of an svg on a web page, or grid within the page, is the upper, left corner: values increase going down. That’s because browsers are more general than data graphics, and with web pages (in English, and many languages) we normally read starting in the top, left and read to the right, zig-zag down, and continue.

Within svg tags, we can place shapes.

The basic shapes³⁵ we can make are very similar to what we use in a language like ggplot, the code is just a bit differently written. Recalling the most common shapes I use, a <circle> uses parameters like ggplot’s geom_circle() (actually this particular geometry is found in a ggplot2 extension package, ggforce). The <circle> example, below, with its attributes just require us to specify the center as an cx, cy coordinate location, and a radius r, then specify attributes like stroke (color), fill, stroke-width, and opacity of the fill or line to alter how it looks:

Along with <circle>, svg provides a <rect>, with attributes like geom_rect(), a <text>, like geom_text(), and a <path>, like geom_path(). And, as with ggplot’s geoms, we can change svg shape attributes like line color, fill color, stroke width, opacity, and so forth.

Because <path>³⁶ is a little more involved, let’s consider it too. Here’s an example:

If you have ever drawn pictures by connect-the-dots, we code an svg <path> like that: a path tag or a path shape is a connect-the-dots, written as a string of letters and coordinates that we assign to the d attribute.

When we start a drawing, before we touch our pencil to paper, we locate the dot marked number 1. In svg code, that’s the command move to, or Mx,y, where x and y are the coordinates where we first put the pencil to paper. Once the pencil touches the paper, we move our pencil to the next x, y coordinate location. That’s the L command in the string above, which means “line to”. And that creates a straight line. Thus, in the above example, our “pencil” made four straight lines forming a rectangle.

Finally, we can make the line curve, the “curve to” command C, not shown in the above example. Now this command takes some practice to get well.

The curve to command, has three x, y coordinate locations. The first two coordinates are “levers” I’ve colored blue and purple here:

The last x, y coordinate for curve to C is just like the Lx,y location: it’s the final place we move our pencil.

Now, svg has significantly more functionality, but that’s all we will discuss for now. And this concludes the basics of how vector shapes are made by other programs under the hood, like ggplot.

Bellamy-Royds, Cagle, and Storey (2018) provides helpful guidance for svg.

3.2.1.7 Canvas

When performance drawing svg shapes becomes an issue—which may occur on slower computers with 1,000 to 10,000 shapes, more with today’s computers—we gain performance by switching to raster graphics. For raster graphics, we draw pixels on canvas³⁷, which we specify within html using the <canvas></canvas> tag, shown below. From pixels, we cannot select shapes or paths like we can with svg graphics, and resolution drops upon zooming into the canvas. If for vector shapes we can edit with Inkscape, for edit rasters, edit with something like Photoshop. Here’s an example <canvas> tag:

3.2.1.8 javascript

Now, html, css, css grid, svg, and canvas all work together to create what you see on the web page. To make them interactive, in other words to change the content or formatting we see, the browser runs code called javascript³⁸. Javascript is a programming language that we (or our software tools) can code to listen for our (inter)actions, and react by changing the html or css or svg or whatever is needed to update in the interacted webpage.

We can bind elements to events that, upon happening, trigger javascript code, which in turn can modify content: html elements and attributes, svg or canvas, or css style. Really it can modify anything in the DOM. As with R packages that abstract and ease our application of specialized functionality, easing the burden of writing code, many javascript libraries are available to do the same.

Here is generic code to bind listeners to elements that trigger changes through functions:

Now the very basic code I’m showing above gets to the heart of how interactivity works. In javascript, we can search the DOM for a named html element or tag, and assign it as an object, here we named it element. And javascript let’s us do things to that object through functions attached to the object (this is an object-oriented programming framework). Here, the function is generically called onevent, but the event part is a placeholder for actions; here are a few specific functions: onclick, or onmouseover, or onkeypress. Our actions. The function watches for our action, on the bound element, and when it sees the action, it calls whatever function is assigned. Here I have generically called it the function functionName. And that function then does things we code, like adding a new tag element, or removing one, or changing a stroke width, or color, or really whatever we want to happen.

And that, on a very simple level, is basically how we achieve interactivity. Now as applied analysts, we may not be coding in javascript directly. Instead, some of our analysis software does, which we discuss next.

To go deeper into javascript, consult Duckett, Ruppert, and Moore (2014) for a basic understanding and Arslan (2018) for a modern, more thorough treatment.

3.2.2 Tools for interactive graphics

3.2.2.1 ggiraph, an htmlwidget

The grammar of graphics — implemented in R as ggplot2 — is currently among the most flexible coding libraries for creating static graphics. We’ve already seen how to use a complementary package with ggplot2 to add animation: gganimate, a grammar of animated graphics. With similar complementary packages, we can specify interactivity. Let’s review a static version of our example of the 30 baseball outfields, and then make it interactive using ggiraph. Here’s the code and graphic:

It’s pretty simple. All the data is is a data frame with each observation being the id of the ball field and connect-the-dots x and y coordinates. And I use geom_path() to draw the 30 black boundary lines. If we’re looking closely, we’ll see that I also have a geom_polygon() and I have subset the data between the two geometries. That’s because I draw the outer black lines with geom_path() but also have the infield brown dirt location information in the data, so I filter that out of the black lines, and I only use the dirt path information for geom_polygon(). And geom_polygon() enables us to fill the polygon with color, here brown.

To make it interactive we can use almost the same code. We include a second package called ggiraph, for this example:

The actual interactive version, of course, is near the beginning of this text, figure 1.

Once we understand the basics of ggplot, it is pretty easy to add interactivity, as we have above. And the website for ggiraph includes other examples of functionality it offers. In this example, we save our interactive ggplot as gg_boundaries and pass it as a parameter into girafe(). Notice, this function gives us options to change css when one of our actions on an element in the graphic triggers a reaction in the code.

Next, let’s share interactivity across this graphic with another for fence heights. To add the second graphic with fence heights, we start by making another ggplot graphic,

but again using the interactive version of the ggplot geom. Again, we save the second graphic into an object. Here I’ve named it gg_fences. To combine the two graphics, we give both plots at the same time to the girafe function.

Of note, in print( gg_boundaries / gg_fences ), the slash is to organize the graphics, and that overloaded function we get from the package patchwork, which is useful for organizing plots. The slash means we are placing one graphic on top of the other, like a fraction with a number on top and bottom. And that’s it. The rest is the same as with one graphic, and now both graphics work together, cross sharing, in this case, the hover action.

Learn more about this tool from Gohel and Skintzos (2021). To learn more generally about htmlwidgets, consult Vaidyanathan et al. (2020). Let’s very briefly consider one more set of tools.

3.2.2.2 plotly

plotly is an R package for creating interactive graphics, and interfaces with the same-named javascript library, plotly.js, which in turn is based on d3.js. R’s plotly has several helpful features. The first of these are, like, ggiraph, allows easy integration with ggplot2. The first function, perhaps, to learn, is ggplotly() which takes as a parameter a ggplot object and makes it interactive. And combined with another package, crosstalk, a plotly graphic can link or bind with other htmlwidgets. Here’s an example, linking it with DT, an R interface to the DataTables widget:

First, we create a key that identifies observations across the graphic and table, which is added to our data frame. That’s the highlight_key() function. Here, our data frame is the mpg example in R. Then we save the keyed version of it in a new object, here I’ve called that, just m. Then, we create our ggplot object, but notice that we use the keyed version of the data frame for our data. Once we’ve made, and saved the ggplot to an R object, we make it interactive. Plotly’s version of this uses two functions, called highlight() and one of its parameters is the ggplot object wrapped in another function called ggplotly().

Both objects are html widgets, which we can place together in a single html file for them to interact. The crosstalk package also includes a helper function that makes it easy to place these objects side by side to view directly when run from RStudio or even the console, even without designing an html page: bscols() creates a browsable html element.

And with plotly, we also get other functionality pretty easy, like zooming and panning, or a filter box, or a radio selection box, and so forth.

Sievert (2020) is very helpful in becoming comfortable with this tool.

3.2.3 Organizing interactive graphics

Now that we have web-based, interactive graphics, we can organize them into web pages using the technologies just discussed: html, css, css grid, and javascript. Now, as with the tools above, we can also abstract the details using tools like r markdown, knitr, and RStudio. We’ve already discussed these in the context of a reproducible workflow, section ??. But we can add r markdown templates for organizing graphics into, say, a dashboard. Enter flexdashboard, another R package.

3.2.3.1 r markdown templates

The flexdashboard template is an r markdown file that creates a grid to place things. The particular grid it uses is called flex grid³⁹ and is, more specifically, a framework called bootstrap4⁴⁰ that sets defaults for a flex grid.

A nice feature with bootstrap4 version of flexgrid is that it is fully responsive to rearranging your content to best fit the size of device the user is viewing, like a desktop versus an iPhone. And we didn’t have to code specifically to achieve this responsiveness.

3.2.3.2 css grid

But next, let’s consider a more, ahem, flexible approach. Flex grid is, perhaps ironically, less flexible than css grid. By that, I mean flex grid only allows us to specify either rows or columns, not both, like we reviewed with css grid. So flex grid is not as precise either. So, now, let’s consider our own widget placement using css grid inside a basic r markdown file.

Here is the original R markdown file.

3.2.4 Combining the technologies — a minimal example

Now, let’s bring these technologies together into a fairly minimal example. For this example, we continue with studying and communicating for Citi Bike. This time, we’ll create a dashboard for Lyft’s head of marketing for the operation of Citibike. Recall, first, from earlier sections, and the three fundamental laws of communication in Doumont (2009c), that we begin by considering our audience and purpose. One helpful place to learn more about marketing executives, their responsibilities (broader than you may think), how they reason about data, and communicate with other marketing executives about data, consult three articles by David Carr, head of digital marketing for Digitas in London: Carr (2019), Carr (2016), and Carr (2018). Re-read them.

Now, of course, what we can learn from David are about him, and perhaps marketing executives in general. We should strive to learn as much as we can about the particular person we plan to communicate with. Here, that would currently be Azmat Ali, Head of Rider Product Marketing at Lyft.

We’ll add to our earlier interactive graphics that showed bike stations, and times they were empty and full. This time, we’ll use pre-ride data from the same time frame (January 2019) and into it merge hourly information on weather: e.g., temperature, precipitation, wind conditions.

We can frame research questions relevant to Ali, and for learning purposes, we’ll categorize them using the graphic of values in Carr (2019). Here are some examples:

Cultural Value | relevance. Are there better temperatures for us to trigger marketing messages to encourage rides?

Customer value | purchase experience. How can we segment our audience to find opportunities for increasing ridership?

Cultural Value | relevance. Are there better times of day for us to trigger marketing messages to encourage rides?

Business value | insight creation. Do any anomalies suggest preferred customer behavior within conditions?

Business value | insight creation. What customer/rider attributes and use cases are more correlated with high usage? How can we use this information to expand our prospect marketing efforts and more effectively appeal to prospects who display similar behaviors?

Business value | insight creation. Similarly, Do rider attributes correlate with lower usage? Are we missing key target audiences?

Customer value / purchase experience. Are there any anomalies in the data that would indicate lack of availability may be causing lower usage?

Let’s now present a few of these questions into an html document containing interactive data-graphics for purposes of exploratory communication. Visit this link to view the interactive. Here’s a screenshot:

To create this example, we used the same technology stack and tools just discussed: an r markdown document,

---
output: 
  bookdown::html_document2
---

that includes css styles,

<style>
</style>

and between those <style> tags, we defined an exact size for the document (.main-container) and css grid classes for each section of content we wanted to place:

.main-container {
  min-width: 1600px;
  max-width: 1600px;

}

a {
  color: #bbbbbb;
}

.gridlayout { 
  display: grid;
  position: relative;
  margin: 10px;
  gap: 10px;
  grid-template-columns: 
    repeat(8, 1fr);
  grid-template-rows: 
    repeat(8, auto);
}

.title {
  grid-column: 1 / 9;
  grid-row: 1 / 2;
  font-size: 30pt;
  font-weight: 900;
}

.lefttoptext {
  grid-column: 1 / 2;
  grid-row: 4 / 5;
  hyphens: auto;
  text-align: justify;
  font-size: 10pt;
  line-height: 1.4;
}

.righttoptext {
  grid-column: 3 / 4;
  grid-row: 4 / 5;
  hyphens: auto;
  text-align: justify;
  font-size: 10pt;
  line-height: 1.4;
}

.leftbottomtext {
  grid-column: 1 / 2;
  grid-row: 6 / 7;
  hyphens: auto;
  text-align: justify;
  font-size: 10pt;
  line-height: 1.4;
}

.rightbottomtext {
  grid-column: 3 / 4;
  grid-row: 6 / 7;
  hyphens: auto;
  text-align: justify;
  font-size: 10pt;
  line-height: 1.4;
}

.rightinteractive {
  grid-column: 5 / 9;
  grid-row: 3 / 8;
}

.instructions {
  grid-column: 5 / 9;
  grid-row: 2 / 3;
  font-size: 10pt;
  line-height: 1.4;
  color: #888888;
  column-count: 2;
  column-gap: 30px;
  hyphens: auto;
  text-align: justify;
}

.citesource {
  color: #bbbbbb;
  text-align: right;
  grid-column: 3 / 9;
  grid-row: 8 / 9;
  font-size: 8pt;
}

Then we used html <div></div> elements with our defined classes as attributes, and within those tags placed our content — which, in one case, includes an r code chunk — (below, shown as ...):

<div class="gridlayout">

  <div class="title"> ...
  </div>
  
  <div class="lefttoptext"> ...
  </div>
  
  ...
  
  <div class="rightinteractive">

  ```{r}
  # r code for interactive graphics placed here
  ```

  </div>
  
  ...
  
</div>

Exercise 26 Identify the varying types of interactivity, how varying elements interact, and from what audience actions the data graphics react. Do the connections between the data seem relevant to the questions presented for exploration?

Next, we’ll consider how we can use the concepts of interactivity throughout longer communications, not just interactivity within and between particular data-graphics.

Helpful references for implementing the details in this section — and for using additional, related tools (e.g., shiny, d3.js, p5.js, processing) — include: (Tominski and Schumann 2020, sec. 4); (Fay et al. 2021); (Janert 2019); (Meeks 2018); (Murray 2017); (Reas and Fry 2014); and (Wickham, n.d.).

3.3 Interactivity, broadened from data-driven graphics to whole communications

To what use — if any — should we make of interactivity? One use, is when a static graphic does not “reveal all the relationships constituted by the interplay of the data” (Bertin 1981) relevant to our intended message. Indeed, this is frequently the case when exploring high-dimensional data. For that, consider Tufte’s advice on a design solution:

At the heart of quantitative reasoning is a single question: Compared to what? Small multiple designs, multivariate and data bountiful, answer directly by visually enforcing comparisons of changes, of the differences among objects, of the scope of alternatives. For a wide range of problems in data presentation, small multiples are the best design solution (Edward R. Tufte 1990a).

We’ve already discussed small multiples, reviewed an example with the Citi Bike data (maps sliced by hour of day), and interactively linked multiple graphics, including brushing and linking scatterplot matrices. Consider, too, trelliscopes (Hafen and Schloerke 2021).

Another use is to adjust the focus of particular data within the context of others. Consider whether we can more compactly represent certain views of the data through interactivity.

Interactivity can enable trust, too, as previously explained by Gregor, CIO of DataWrapper.

We should ask: can interactivity simplify, clarify, provide focus to the contextual comparisons in our messages, or otherwise allow our audience to “test” relationships with their own choice of views?

With our understanding of the foundations of interactive, data graphics, and tools to make and organize them, let’s focus now on how we can guide our audience through entire interactive communications.

3.3.1 Flow factors

McKenna et al. (2017) has studied the ways skilled practitioners guide audiences — visual narrative flow — and categorizes some approaches into “flow factors”. These include navigation input, level of control, navigation progress, story layout, role of visualization, story progression, and navigation feedback. Let’s consider these in turn.

Navigation input is the way or ways a user progresses through a communication. Common approaches are through scrolling, clicking buttons, or dragging sliders.

By level of control, McKenna means the audience’s control over any changes to the document, whether text, data graphics, or other components. Control can be discrete or continuous.

Navigation progress refers to how an audience perceives where they are within the communication. Web browsers generally provide some indication by default through the scrollbar. But other common approaches are to show a series of dots, each representing some conceptual section of the communication.

The story layout refers to the visual appearance and organization of the communication. We can use one or multiple columns of information, we can organize the overall information vertically like a document, horizontally or stacked like a slide show, or use some hybrid of these.

The role of visualization is the purpose that they serve in a communication or narrative. Are they the primary focus with annotations helping the audience through it? Do they serve to illustrate some smaller component within an overall narrative? These are the questions we ask about the roles played by our data graphics.

Story progression refers to the one or more paths for a story to unfold. These paths may be temporally and spatially linear, temporally or spatially reversed, they may skip parts of sequences, or be some blend of these ideas. Linear paths may be effective through scrolling, while non-linear paths may benefit from use of, say, a button to jump from section to section representing time or space.

Finally, navigation feedback are the way or ways the interactive document shows the audience how their input affects the communication.

McKenna et al. (2017) in their study, collected numerous examples of each of the above. Along with studying those, review the interactive communications cited in Hohman et al. (2020) to see how those interactive communications approach the above concepts.

We should keep in mind that, just as static graphics require text, so too, do interactive graphics.

And interactive documents that explain, especially using the above concepts like scrollytelling or clicking for details on demand can lead to better audience recall. See Schneiders (2020).

3.3.2 Preserving the principle of proximity

3.3.2.1 Folding details on demand

Let’s consider a potentally helpful feature: enabling the audience to click to show additional details within a html, as discussed in Hohman et al. (2020). Some implementations can be simple:

The triangle beginning this sentence, when you click it, provides details on how to implement its functionality of hiding and showing additional information.

We can “fold” any type of information, and the functionality is commonly used to allow an audience to review code — by clicking or unfolding — associated with a result (like a graphic) in the main document view. We create folding with just two pairs of html tags. The outer tags are <details> … </details> and within these, we first place the words shown with the triangle between <summary> … </summary> and follow that with the information. To learn more, consult MDN Web Docs. <details>: The Details disclosure element.

Having multiple levels of details accessible to our audience through basic interactions can help us, in some ways, to keep related content closer together, and also help focus audience attention on our narrative. Scrollable interactions provide another way.

3.3.2.2 Scrollable interactions with the DOM

To motivate one basic use of a scrollytelling document, consider our experience in any recent textbook where significant narrative was needed to understand a data graphic. Best practices where less narrative is involved, as we’ve discussed, is to integrate the data graphic directly into the paragraphs. And this follows the principle of proximity: keep related information spatially together. But the concept breaks down when significant narrative is required to explain the data graphic. Typical approaches number the figure and then in the narrative, even pages later, refer back to that graphic. The audience needs to go back and forth between the locations. The concept of scrollytelling is a potential solution in some cases. We can freeze the data graphic in place, and scroll the narrative beside the data graphic, explaining new aspects as the paragraphs move along. The principle of proximity is preserved. And with the modern technology stack, it’s getting easier to accomplish. Let’s see a minimal working example.

Let’s place a minimal wireframe of a scrollable explanation inline below. Make sure the top of the inline frame is visible in your browser viewport, and take a moment to review:

Here is the original R markdown file.

Notice that as we scroll the document, the three figures each freeze as they come near the top of the inline frame while the narrative article paragraphs continue scrolling past. Then, when all paragraphs for a given data graphic move past the data graphic, the graphic leaves the top of the view with that final explanation. Then, another section containing a new data graphic comes into view with its own paragraphs. That graphic, too, freezes until all its paragraphs scroll past, and so forth.

The basic technology stack isn’t too difficult, and only requires a few lines of html and css to get working:

First, as shown, the <figure> element must have “empty” space inside the <section> element. Think of these elements like physical boxes, a small box inside a larger box. We could move the larger box to and fro and the inside box would move (or scroll) with it. Or, by adding the css code position: sticky with a sticky location at top: 5rem,⁴¹ we suspend the <figure> element within the <section> element such that the figure remains in place while the outer <section> box moves. But when either side of the outer box contact the inner <figure> box, it pushes that inner box along with it. Here’s the r markdown file to reproduce the above example.

Of note, just as we may place these interactive scrollable explainers of data graphics inside the inline frame, above, with <iframe>⁴² html tags, we may also place the scrollable explainers within any css grid area we define, enabling almost limitless layouts.

Holding graphics in place as explanations scroll by are one important way we can employ document-level interactivity. First, as with data-graphics more generally, the graphics we hold in place may be interactive, whether of the htmlwidgets variety or made with d3.js or svg, among other available technologies. Second, these technologies also enable our audience actions to not only change the graphic locations or switch graphics, but we can link those actions to changes within that htmlwidet or d3.js graphic.

3.3.2.3 Interactions with data graphics triggering changes to the DOM

We just considered how to enable interactions to flow from the DOM to, for example, placement of its data graphics and text to preserve the principle of proximity and guide our audience.

We can also enable interactions to flow the other way, where data graphics made with the technologies discussed in section ?? can trigger changes to the DOM using event listeners and javascript.

Using ggiraph, again, to illustrate this type of functionality, its geoms natively include an onclick listener that can trigger custom javascript. From an onclick, then, we can trigger our own javascript functions that we include between <script> tags in the html, which in turn contains our ggiraph data graphic htmlwidget. Our triggered function can, say, add or remove custom css classes to an element in the html, add or remove elements, load other documents or images within an iframe or scroll text in another grid column to a new location, just to name a few of limitless options. Really, once we have the data graphic trigger javascript, we can design any modern idea using web technologies. Let’s set up a couple of examples. For a first, example, Click a circle below to trigger an onclick event that calls a javascript function, passing it a data value, and the function adds css formatting to some text in the DOM:

This text will change when you click a circle.

Click the triangle to see the code implementation below.

The above example is contained in this text, which is an html file. It includes this data graphics code within an r markdown code chunk:

set.seed(1)

df <- 
  data.frame(
    x = rnorm(5), 
    y = rnorm(5), 
    ID = seq(5))

p <- 
  ggplot(
    data = df, 
    mapping = aes(x, y)) +
  theme_void() +
  geom_point_interactive(
    size = 5,
    onclick = paste0("myFunction(", df$ID, ")")
  )

girafe(code = print(p))

The function it calls, myFunction(), is within <script> tags, like this:

<script>
function myFunction(info) {
  var el = document.getElementById("myDIV");
  el.classList.add("mystyle"); 
  el.innerText = "The clicked circle's ID is " + info + ".";  
}
</script>

The css style class we invoke (mystyle) looks like this:

<style>
.mystyle {
  color: purple;
  font-weight: 900;
}
</style>

Finally, here is the <div> element we identified as “myDIV”:

<div id="myDIV">This text will change when you click a **circle**.</div>

If we wanted our javascript function to load some document in an iframe, we might set it up this way:

<script>
function myFunction(page) {
  document.getElementById("iFrameName").src = page;
}
</script>

where page is the name of the file (like an svg or html) we pass to myFunction() inside the onclick event listener. The corresponding iframe element in the html might look like:

<iframe id="iFrameName"  data-external="1"></iframe>

Clicking the above triangle again will hide, or fold away, these details.

---

This functionality isn’t exclusive to ggiraph; we just used it for illustration. plotly provides similar ways to trigger custom javascript, which is explained in Sievert (2020). So do other htmlwidgets.

3.3.3 Interactivity to guide our audience

3.3.3.1 Help with flow

Communication educators recognize that documents are frequently organized for the author instead of for their audience (Doumont 2009b). The problem is so prevalent that with documents generally, and especially academic articles, audiences are advised to read information out of order to be more efficient with consuming the information (Pain 2016).

That may not, however, be what we as authors who follow best practices prefer or what we believe is best for our audience. Yet we have no control over how ordinary documents are consumed. Interactive documents can help us. Along with preserving the principle of proximity, interactive documents can help us guide our audience through our preferred ordering of narrative. There are many approaches, but consider that the scrollytelling layout just described, by freezing material at a location during portions of the audience’s scroll does suggest the material be read before the next section, even if the feature does not prevent an audience from skipping the material entirely.

One a general note, the best designs become invisible to our audience to let them fully absorb and engage with our content. Having these concepts front of mind as we create interactive communications will help us help our audience achieve flow⁴³. That should be our goal.

…

3.3.3.2 Help with interactions

Some interactions may be difficult, even when their affordances are well explained and understood. Since scatter plots in various forms are both extremely important and common in data analyses, let’s consider how to improve our user experiences through an example in that taxonomy. In a scatter plot, various constrants — such as ensuring precision in decoding — may limit how we design our visual encodings.

To make the issue specific, let’s say we have a scatter plot in which measurements are positioned along an x and y axis, and we are constrained in how large we draw these observed points, either by how accurately we need our audience to locate each point’s units of measure along the x and y axes, by the spatial density of those points, or both. The smaller the points and the closer they are together, the more difficultly our audience will have in hovering or clicking on that point as a means to obtain details (like in a tooltip), filter or focus on specific encodings.

Let’s consider an example. First, we simulate some data: for each x and y value of 20 observations, we show on the graph below, and allow the user to hover to learn more information:

Now, let’s see if we can improve the user’s experience in hovering over the observation to gain information. One creative approach that commonly improves user interaction is to overlay another very special geometry called a Voronoi diagram⁴⁴. A Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. In the context of our example, we divide the space between observations equally distance from each x and y location. We’ll just use the euclidean as our measure of distance, but special cases may invite other ways to measure.

We next partition the spaces, shown below⁴⁵:

Notice how much easier it is for the user to hover over an intended selection. They no longer have to be precise, just closer to that point than any surrounding points. We’ve left visible the partitions for teaching, but we may remove these to improve readability:

In this example, and those similar, overlaying an interactive Voronoi diagram is a very useful and creative approach to improving user experience. We used this technique for user interaction in our working example for Citi Bike: interactive version of Spencer (2019a).

Take the time to find similar, creative approaches to problem-solving other issues with user experience, too.

4 Multimodal communication and audience studies

4.1 Verbal narrative with data graphics

Until now, our discussions of narrative, visualization, and interactivity assume that the communication must stand on its own to deliver our messages to our audience.

But sometimes we may want to combine our data-graphics with a verbal narrative. Doumont (2009a) motivates oral presentations as,

Oral presentations are about having something to say to one’s audience and being able to say it in an articulate way while looking them in the eye. They are about engaging the audience with mind and body, conveying well-structured messages with sincerity, confidence, and, yes, passion. They are about presence, about being seen and being heard, not about having the audience look at slides that are in fact written pages, while hoping not to be noticed.

Perhaps we present orally for those reasons. But let’s consider two more. First, we are all social, and can benefit from having a direct, human connection to the material we care about. Second, from a communication efficiency standpoint, we have a direct feedback loop in real time through each aspect of the narrative we present, if we’ve prepared to enable that loop. And having direct feedback at the time of the communication can be extremely valuable, leading to more rapid progression of the ideas presented.

In those circumstances, we should adjust how we provide our explanations and visuals, and we have multiple options. First, we should consider whether our audience would benefit from pre-presentation review of important material and, if so, how we should craft that material. Second, we should consider whether, if at all, we should adjust how we visualize and explain our information during the presentation. Here, we consider both issues, in turn.

4.1.1 (Pre-)meeting preparation

Edward Tufte has advocated for beginning meetings with a detailed written (paper or electronic) document with the expectation that our audience reads them before a discussion, so that the meeting itself can become a more productive dialogue with deeper understanding. Most recently, he provides a chapter-length treatment of the idea in Edward R. Tufte (2020). Here, he sketches out constraints: the document “should be 2 to 6 pages long, written in sentences, with appropriate images and data displays. Do not send out your stuff in advance, people won’t read it.” He explains why:

Audience members read 2 or 3 times faster than you can talk. The document is in hand, everyone in the audience reads with their own eyes, at their own pace, their own choice of what to read closely.

In contrast:

In sllide presentations, viewers have no control over pace and sequence as the presenter clicks through a deck — viewers must sit in the dark waiting for the diamonds in the swamp.

Then why are you there?

Your job is to provide intellectual leadership, which is why you are making the presentation.

Doumont (2009a), too, recommends companion documents to presentations. Along with Tufte’s above advice, he offers five thoughts. First, content and credibility: “your audience seeks to learn What is the substantive content? What are the reasons to believe the presenter?” Thus, our document and presentation should explain the problem, its relevance and the so what, and our next steps for resolving the problem. To be credible all content must not just be truthful, but it should also cite sources, including data, quote experts on the specific issue, and reveal any potential biases.

Second, and his next point has been front and center in many of the earlier sections, we should think about our audience. Along with what we’ve considered, do not underestimate our audience. Do not “dumb things down” but, instead, respect their intelligence. Third, when you present after the audience has read your document, “do not repeat”do not merely repeat what they read.” Instead, go more in-depth, and refer back to the document paragraphs where relevant to tie together the two channels of information.

Fourth, practice your presentation ahead of time! More than once! Consider writing it out word for word, then speaking it aloud to get a feel whether the written sentences feel like natural spoken language, and to have an estimate of how the time required for presenting it verbally. And part of aloud rehearsal is to include white space — silence — for your audience to process your messages.

Finally, respect your audience’s time: finishing early is better than finishing late!

All these ideas can be helpful in particular contexts. But consider a course I teach in Columbia’s graduate program — Storytelling with data — and the pre-lecture study of primary source material, guided in part by this text. This occurs by necessity before discussion, before class. Primary-source material, for the most part, does not fit within Tufte’s recommended six pages for that which we cover during a weekly session. Certainly, one aim of the text before your eyes is to provide summary of various source materials, as well as highlight important ideas. Yet students are expected to prepare ahead of time.

Let’s turn, now, to the post-study presentation and, specifically, how to incorporate verbal communication and data-graphics.

4.1.2 Verbal with the (data) visual

4.1.2.1 Limitations with multi-modal communication

To motivate the value of time working on design of presentations, consult Edward R. Tufte (2006b). In fact, after considering Tufte here, we may be wondering whether slides are even a good idea:

PowerPoint, compared to other common presentation tools, reduces the analytical quality of serious presentations of evidence.

This is especially the case for the PowerPoint ready-made templates, which corrupt statistical reasoning, and often weaken verbal and spatial thinking.

To answer that question, we may consider how Tufte himself has conducted presentations, as at E. Tufte (2016). It’s worth watching, and in it, you’ll find he does use presentation visuals! Edward R. Tufte (2006b) provides reasoning. First, PowerPoint (still, today) has poor default formatting for any slide you intend to create, and encourages things like excessive bullet points or the equivalent to what we considered with data visuals: let’s call it slide-junk. Secondly, slides as presented can be very low resolution compared to paper, most computer screens, and the immense visual capacities of the human eye-brain system (id). With little information per slide, many slides are needed. Third, information stacked in time makes it difficult to understand context and evaluate relationships (id). Visual reasoning usually works more effectively when the relevant evidence is shown adjacent in space within our eye span. This is especially true for statistical data, where the fundamental analytical task is to make comparisons (id).

When designing visuals for a verbal narrative, use the right tool for the information. As Tufte explains, Many true statements are too long to fit on a slide, but this does not mean we should abbreviate the truth to make the words fit. It means we should find a better tool to make presentations. Secondly, increase data-ink on slides too, within reason. Doumont echos this point (as do I):

A major noise source on slides is text, especially a lot of text, for the audience cannot read one text and listen to another at the same time. An effective slide gets the message across (the so what, not merely the what) globally, almost instantly. There lies the challenge: to express a message unambiguously with as little text as possible. Visual codings being in essence ambiguous, effective slides almost always include some text: the message itself, stated as a short but complete sentence. Besides this text statement, the message should be developed as visually as possible: this development shoiuld include only whatever words are necessary for the slide to stand on its own.

Beyond including no superfluous information in their design, slides should include no superfluous ink in their construction. Optimal slides get messages across clearly and accurately with as few graphical features as possible: they are noise-free (Doumont 2009a).

Along with Doumont (2009a), Schwabish (2016) provides helpful general advice for designing visuals for presenting. To be sure, the broad strokes all paint what we’ve canvased previously. Again, per Doumont: get our audience to pay attention to, understand, and (be able to) act upon a maximum of messages given constraints. Indeed, as Doumont correctly notes, most slide visuals contain too much text. Period. When asking ourselves whether we’ve over-texted, consider whether we have created the slide for our own understanding, perhaps in part as speaking notes? Don’t do that. You may have notes, but they do not belong on your visuals, and do not show them to your audience. Second, are the slides to be presented to double as a written report? Don’t do that, either. Instead, if dissemination is important, create the aforementioned document, with full sentences, paragraphs, and a coherent narrative. If you must, you may also key the document to the slides. Or, less ideal, when circulating the slides after the presentation, include a (perhaps lightly edited) transcript of your verbal narrative. For examples of transcripts with visuals, see Corum (2018) and Corum (2016)⁴⁶. But well-created presentation slides would not, in most cases, adequately explain their context without our verbal narrative. Third, if we find ourselves copying from written documents onto presentation visuals, perhaps because we’re running low on time, consider that this approach is not better than nothing. If the words distract your audience from listening to you, if your words are competing with those on your visuals, those visuals are worse than none at all.

4.1.2.2 Strategies for verbally communicating data-graphics

If text on visuals compete for attention with our verbal narrative, and the general advice above is use as few words as possible, how should we think about the lengthy advice in data graphics to annotate and explain, in this context?

That advice still applies! But some of the annotations and explanations are now verbal. We have two helpful strategies in thinking about how much explanation we place on data graphics that support verbal communication. As an initial matter, we much understand what pace to provide material to our audience.

With pace in mind, we can, first, verbally explain what the data visual shows. In fact, a best practice is to verbally explain what the audience is about to see before you show them. And, second, we can layer information, chunk-by-chunk, onto and around the data graphic, so that the audience only needs to understand small bits at a time, and each subsequent portion is added as a new layer within the context of what the audience just learned.

4.2 Processes for user-centered, content design

Throughout this text, we’ve focused on purposeful communication with specific audiences. We’ve discussed approaches to structure narrative, text-based communication through writing and rewriting. We’ve discussed approaches to integrate both numbers and data-graphics into those narratives. And we’ve discussed the why and how to provide our audience with interactivity in those narratives.

But no communication is perfect, even after our re-writes. Here, we overlay an iterative plan to move towards better communication for its purpose and audience.

In laying out these ideas, I borrow from Ko (2020), Richards (2017), and Hartson and Pyla (2019), which can be understood, at least in part, as describing communication from a designer’s perspective. These offer a principled approach to problem understanding, creativity, prototyping, and evaluating.

4.2.1 Problem understanding

A problem is specific to an individual; at its most basic, a problem is simply an undesired situation or context for that person. There is no such thing as an average person, and an undesirable situation for one person may, in fact, be desirable for another. But, generally, the more individuals we move to a more preferred situation, the more value our iteration toward a solution. To understand individuals’ problems, we can survey, interview, observe, or study research of others. Each of these can have advantages and limitations and can be a subject of study in its own right, see for example Rubin and Rubin (2012).

Interviews, as we know, are the direct, synchronous questions we pose to another, listening to answers that become information — data — to the point of our inquiry. The quality of the answers depend on the quality of our questions. With questions, then, do not lead your audience; instead, be neutral. Second, don’t include assumptions within, or imply any answers to, your questions; don’t so risks the response just reflects your question rather than the true circumstance. Finally, keep questions focused, clear, and logical. But note a few of the many limitations with interviews. Answers are taken out of context, meaning they require the audience to recall information. Secondly, the answers may be influenced, or biased, by context.

Instead of asking someone — or along with asking — we can observe our audience in the context of the problem of which we’re focused. Observations can be with or without audience awareness of the observation. Awareness can influence what we observed (behavior may depend on observation, for many reasons). But awareness also allows our audience to explain things more directly while we observe, and allow us to form questions to better understand what we’re observing.

Both of these approaches, however, can be hard to generalize from the individual to groups. Surveys and secondary research⁴⁷ on prior studies provide yet more alternative methods to learn problems and formulate potential solutions for designing communications.

From another perspective, and in both forming and framing the research above, we can identify our audience through user stories and job stories. For both, Richards (2017) provides us with a template or simple framework to begin. Here’s a fill in the blank for user stories:

As a [person in a particular role]

I want to [perform an action or find something out]

So that [I can achieve my goal of …]

This framework can help us be more specific in getting started. Placing the concept into one of our working examples, Citi Bike, one user story could look like this:

As a [marketing executive]

I want to [explore associations between subscriber attributes and contextual preferences]

So that [I can improve upon our segmentation and targeting]

Or another of our working examples, the Los Angeles Dodgers:

As a [marketing executive]

I want to [understand variation in game attendence conditional on expected outcome and contextual factors like day of week, opposing team, starting pitchers, and cumulative win percentages]

So that [I can increase game attendence within constraints]

For these user stories to be valid, we would need to first research relevant marketing executives, if possible, at Citi Bike or the Dodgers, respectively. The value of this approach increases as we develop multiple actions and goals for a given user, or multiple users, each needing a tailored communication.

Similarly, and alternatively, we may find that framing our communication purposes in terms of jobs work better to help us become specific. Richards provides a template here too:

When [there’s a particular situation]

I want to [perform an action or find something out]

So I can [achieve my goal of …]

Framing our research into these forms can help us to be specific in defining our purpose and audience for communicating.

4.2.2 Creativity

Effective communication, too, requires creativity. But how? Nobel-prize winner Linus Pauling, foreshadows the how, when he explained,

The best way to have a good idea is to have a lot of ideas.

Indeed, we find a something idea from Bayles and Orland (1993), in an experiment conducted on students to learn about creativity:

The ceramics teacher announced on opening day that he was dividing the class into two groups. All those on the left side of the studio, he said, would be graded solely on the quantity of work they produced, all those on the right solely on its quality. His procedure was simple: on the final day of class he would bring in his bathroom scales and weigh the work of the “quantity” group: fifty pounds of pots rated an “A”, forty pounds a “B”, and so on. Those being graded on “quality”, however, needed to produce only one pot —albeit a perfect one —to get an “A”. 

Well, came grading time and a curious fact emerged: the works of highest quality were all produced by the group being graded for quantity. It seems that while the “quantity” group was busily churning out piles of work—and learning from their mistakes —the “quality” group had sat theorizing about perfection, and in the end had little more to show for their efforts than grandiose theories and a pile of dead clay. 

Creator of the ubiquitous javascript library d3.js and former graphics editor at the New York Times, Michael Bostock (2014) applied similar advice, explaining that “design is a search problem.” In that keynote, Bostock led us behind-the-scenes in the creation of several data-driven articles at the New York Times. He showed us hundreds of snapshots of prior versions of what became the final, published articles. The flip-book style presentation of these snapshots show hundreds of ideas tried before the graphics and narrative became final. He advised that early in the search for a communication solution, use methods that allow fast prototyping so that we can, one, try many things, and two, not become too attached to any particular design.

Let’s look at ways to prototype the communication next.

4.2.3 Prototyping

Prototypes are not the communication. It isn’t polished. It isn’t generally pretty. Its purpose, as Ko (2020) explains, is merely to give you, as a creator, knowledge and then be discarded:

This means that every prototype has a single reason for being: to help you make decisions. You don’t make a prototype in the hopes that you’ll turn it into the final implemented solution. You make it to acquire knowledge, and then discard it, using that knowledge to make another better prototype.

Because the purpose of a prototype is to acquire knowledge, before you make a prototype, you need to be very clear on what knowledge you want from the prototype and how you’re going to get it. That way, you can focus your prototype on specifying only the details that help you get that knowledge, leaving all of the other details to be figured out later.

With just text, we might call a prototype an outline.⁴⁸ As we bring in data graphics — and especially when we layer in audience interactivity with both data graphics and its containing documents — the creation of those interactions can become more complex, take longer to implement. To save time, it can help to sketch out the layout and organization of the information and interactivity. And sometimes the fastest way to iterate though ideas is to set aside the technology, for a bit, in favor of pencil and paper (or, perhaps, any electronic equivalent like sketching software based on touch screens). Information designers Nadieh Bremer and Shirley Wu provide enlightening examples of early pencil sketches in their recent book, Bremer and Wu (2021).

Of note, with sketches, we can sometimes find use in linking them together through storyboards, commonly organized as a grid with visual and narrative elements,

as a way to communicate a larger, graphics-heavy narrative.

At some point, we shift from low-fidelity, hand-drawn prototypes to those of higher-fidelity, using some kind of layout or drawing software. Anything that would allow us to quickly draw things. Apple Keynote, perhaps. Or more specific drawing, illustration, or prototyping software like Illustrator, Sketch, Affinity Designer, Inkscape, or Figma. There is no best tool, and better tools depend on its user’s skill and speed with it, and the purpose it furthers. Of note, what serves as faster is also relative. Bremer and Wu frequently use ggplot2 and Vega-Lite to prototype interactive data graphics that are ultimately coded in the javascript library d3.js.

4.2.4 Evaluating

In the last segment of our circular loop of iterating, we evaluate the communication. We have several approaches, which may be combined. These include critique and empirical research.

4.2.4.1 Critique

Visualization criticism is critical thinking about data visualization. The same is true, more generally, about communication. A critique is a two-way discussion. Stated differently, there’s a human on both sides of the communication. As Richards (2017) recognizes, “it’s not easy to let other people tear your work to shreds. It’s not easy listening to them tell you what’s wrong with [your draft work].” She provides rules to help. First, “be respectful: everyone did the best job possible with the knowledge they had at the time.” Second, “only discuss the content, not the person who created it.” Third, “only give constructive criticism: ‘that’s crap’ is unhelpful and unacceptable.” Fourth, “no one has to defend a decision.” The focus of a criticism is only in making the content better.

Keep these ideas, and Richard’s rules, in mind. First, establish the purpose of the critique. When reviewing someone else’s document, center yourself on the purpose that was agreed upon, such as clarity, accuracy, or correctness. Should this purpose be multiple, review one aspect at a time, focusing on content first.

Secondly, be objective and well-reasoned. Typos are usually more conspicuous than reasoning flaws, but also less important. Each statement should be objective, delivered in neutral language, and backed up by theoretical reasoning or empirical evidence.

Third, offer alternative solutions. In your comments—help, don’t judge. A critique must serve the goal. Simply pointing to problems is not enough. The critic must state an alternative solution in a way that is clear and complete enough to provide a basis for improvement.

Fourth, structure the review. Begin by providing a global assessment, to place further comments in proper perspective. As a rule, point out the weaknesses, to prompt improvements, but also the strengths, to increase the authors’ willingness to revise the document and to learn. 

And a note for the content creator: you don’t have to apply suggestions by the critic, but you should think critically about the advice.

Brath and Banissi (2016) and Kosara (2007) provide a framework for critiques in the context of data visualizations. More broadly, Ko (2020) and Richards (2017) guide us with critiques in the context of design. And in the context of communication, consult Doumont (2009d).

4.2.4.2 Empirical research

The value of critiques depend largely upon the expertise of the critic. Another, approach, used often in industry, is to conduct experiments — industry commonly calls them A/B tests — where one group receives a base design or communication (the control group) and another group receives the same communication but with one modification (the treatment group). This is, in effect, observing the effect of that portion of the communication: how did the change in communication affect the response?

With interactivity, we may wish to include observation or user testing. We can provide the communication to a user, let the communication stand alone (i.e., don’t guide them, verbally or otherwise, outside the communication or interactivity being tested, and ask them to verbalize what they are thinking and how they are interacting. If they become silent, prompt them again to verbalize. This approach can help us understand when and how a communication breaks down in some way. Finally, have them reflect on their interaction with the communication.

---

Lee et al. (2015) provide another view into the process of telling data-driven stories, in the context of a team effort. The authors diagram steps, components, and responsibilities:

But whether we are part of a team or creating alone, we integrate numerous concepts to effectively communicate data-driven, visual narratives. The goal of this text was to introduce many of the main components shown above while providing an entry point for further discovery in whatever rabbit hole you’d like to explore within.

In closing, to paraphrase Richards (2017), storytelling with data “isn’t just a technique,” or set of techniques, “it’s a way of thinking. You’ll question everything, gather data and make informed decisions. You’ll put your audience first.”

Acknowledgments

---

1. For a wonderful reference for using previous writings and works to drive research, consult J. Harris (2017), as we will do when covering this use later.↩︎

2. Abstracting out how to create a graphic lets us focus on what to create.↩︎

3. Note the plural. While we have identified a single person in the memo examples, discussed later, those memos may be passed to others on his team — it may have secondary audiences.↩︎

4. Examples of those with similar needs may categorically include, say, the intended audience in (Caldeira et al. 2018).↩︎

5. We will discuss this structure — old before new — in detail later.↩︎

6. An expectation is specifically defined in probability theory. To optimize is also a specific mathematical concept.↩︎

7. William Zinsser: A long-time teacher of writing at Columbia and Yale, the late professor and journalist is well-known for putting pen to paper, or finger to key, as the case may be.↩︎

8. This form of narrative has dominated since Aristotle’s Poetics, but narrative is broader. See (Altman 2008).↩︎

9. For example, (Snyder 2013) or (Booker 2004).↩︎

10. Later, we will formalize discussion of questions, among other things, as tools of persuasion.↩︎

11. For a detailed understanding of narrative, consult seminal and recent work, including (Altman 2008); (Bal 2017); (Ricoeur 1984); (Ricoeur 1985); and (Ricoeur 1988).↩︎

12. Orwell (2017), for example, argues against political tyranny.↩︎

13. Indeed, we are being warned to abandon significance tests (McShane et al. 2019).↩︎

14. Seminal works on metaphor include (Farnsworth 2016); (Kövecses 2010); (Ricoeur 1993); (Lakoff and Johnson 1980).↩︎

15. Their very-short, classic book on writing would not be in its 50th Edition were it not still valuable. Leading by example, this tiny book provides dos and don’ts with examples of each. Re-read.↩︎

16. In doing so, he introduces another idea, inside out plots, which reverse a table’s numbers and labels in certain contexts.↩︎

17. We will cover other Gestalt and design principles later. Many great references discuss Gestalt principles e.g., (Ware 2020), usually in the context of design generally or data visualizations, but these apply universally: including for tables!↩︎

18. For an example implementation, in R, and more details, see Vaidyanathan, Russell, and Watts (2016) and Kowarik, Meindl, and Templ (2015).↩︎

19. Other implementations of graphics will typically name the components of a graphic similarly.↩︎

20. Note that <...> is not part of the actual code. It represents, for purposes of discussion, a placeholder that the coder would replace with appropriate information.↩︎

21. Jacques Bertin was a French cartographer and theorist, trained at the Sorbonne, and a world renowned authority on the subject of information visualization. He later assumed various leadership positions in research and academic institutions in Paris. Semiology of Graphics, originally published in French in 1967, is internationally recognized as a foundational work in the fields of design and cartography.↩︎

22. In-depth reviews are in Ware (2020), Bertin (1983), Meirelles (2013), and Healey and Enns (2012).↩︎

23. Same as Hue-Saturation-Brightness.↩︎

24. Indeed, most criticisms of Tufte’s work misses the point by focusing on the most extreme cases of graphic representation within his process of experimentation, completely losing what we should learn — how to reason and experiment with data graphics. Focus on learning the reasoning and experimentation process.↩︎

25. Edward R. Tufte (2001b) analyses Minard’s graphic, declaring it, perhaps, the greatest ever created.↩︎

26. Note that in this toy example the “priors” or “unobserved variables” \(\alpha\), \(\beta\), and \(\sigma\) are distributed \(\textrm{Uniform}\) over infinity, which is what the above lm() assigns. This is poor modeling as we always know more than this about the covariates and relationships under the microscope before updating our knowledge with data \(x\) and \(y\).↩︎

27. Interestingly, Darwin’s “survival of the fittest” did not appear until the fifth edition.↩︎

28. We used Petukhov, van den Brand, and Biederstedt (2021), which works well with ggplot objects in R.↩︎

29. See MDN Web Docs. Document Object Model (DOM).↩︎

30. See MDN Web Docs. HTML: HyperText Markup Language.↩︎

31. See MDN Web Docs. box-sizing.↩︎

32. See MDN Web Docs. CSS.↩︎

33. See MDN Web Docs. CSS Grid Layout.↩︎

34. See MDN Web Docs. SVG: Scalable Vector Graphics.↩︎

35. See MDN Web Docs. Basic Shapes.↩︎

36. See MDN Web Docs. Paths.↩︎

37. See MDN Web Docs. <canvas>: The Graphics Canvas element.↩︎

38. See MDN Web Docs. JavaScript.↩︎

39. See MDN Web Docs. CSS Flexible Box Layout.↩︎

40. For general information on the framework, see MDN Web Docs. The particular implementation uses a 12-column layout.↩︎

41. rem is a relative unit of measure, just like px for pixels is an absolute unit. See MDN Web Docs, CSS values and units.↩︎

42. The HTML Inline Frame element (<iframe>) represents a nested browsing context, embedding another HTML page into the current one. For more information, see MDN Web Docs. <iframe>: The Inline Frame element.↩︎

43. See Csikszentmihalyi (1991) and Csikszentmihalyi (2014).↩︎

44. A Veronoi diagram was named after its creator, a Russian Mathematician.↩︎

45. Various software functions are available to perform the calculations. In the example below, we use the function polyclip() in the same-named package, and then plot the resulting polygons using ggiraph’s geom_polygon_interactive().↩︎

46. Jonathan Corum’s presentations provide helpful guidance in their own right, too.↩︎

47. We touched upon basic references to generally or categorically learn a bit about a few audiences in section ??.↩︎

48. An outline is actually a great place to begin even for data graphics and interactions.↩︎