Available records

A world, governing body for running events — World Athletics — maintains records for various distances. To be a reliable and comparable record, the run must comply with certain conditions. Those records include, among other things, the event distance and run date, competitor’s name, date of birth, nationality, the marked time, and a world ranking. These events include short and lond distance, and indoor and outdoor.

Along with these data, single-age world records are maintained for longer distance events, from 3,000 meters to marathon, by The Association of Road Racing Statisticians (ARRS). ARRS is an independent, non-profit organization that collects, analyses, and publishes results and statistics regarding elite distance running at distances 3000m and longer. Here are the observed measures:

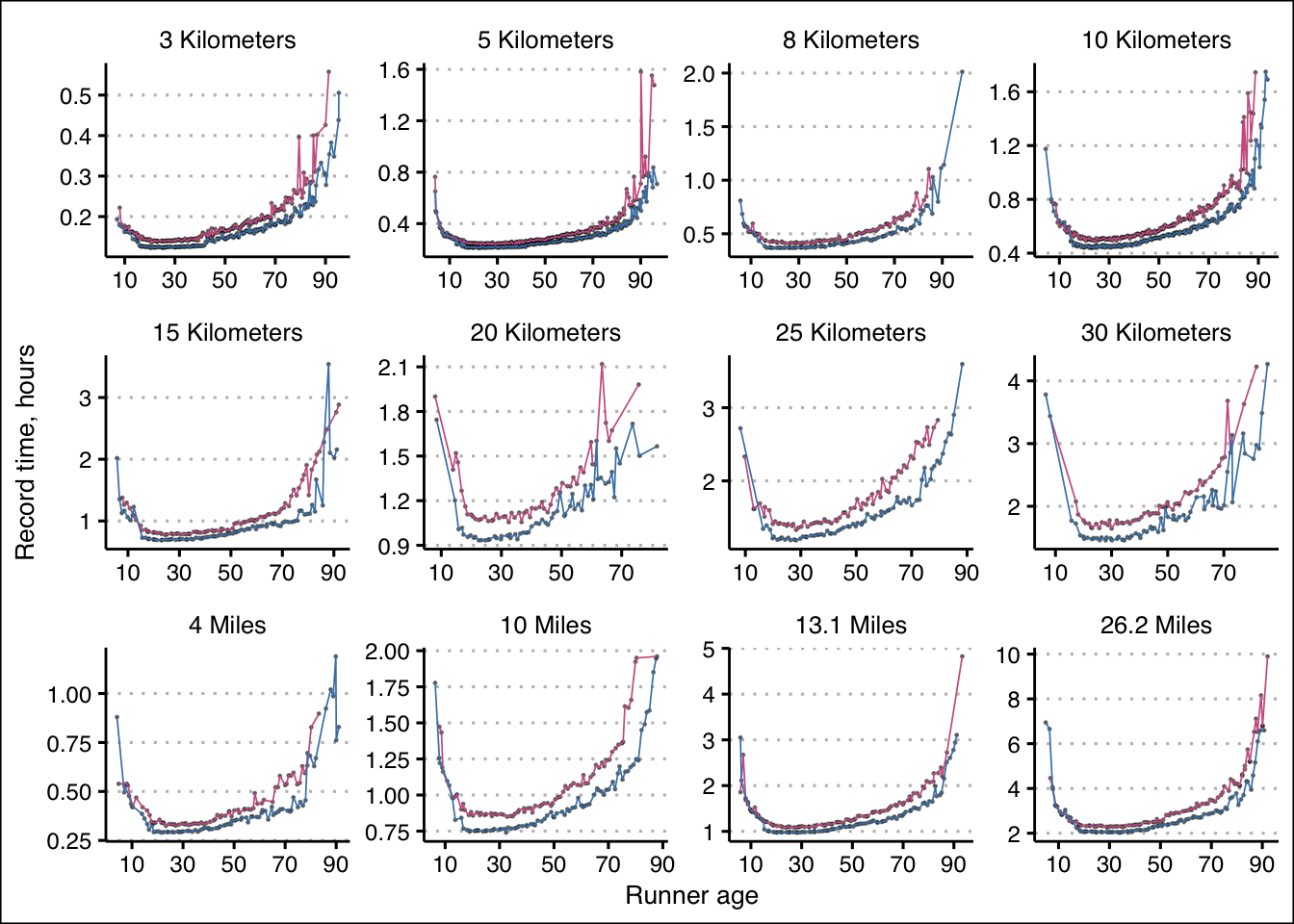
Let’s review the single-age record data for all race distances and gender:

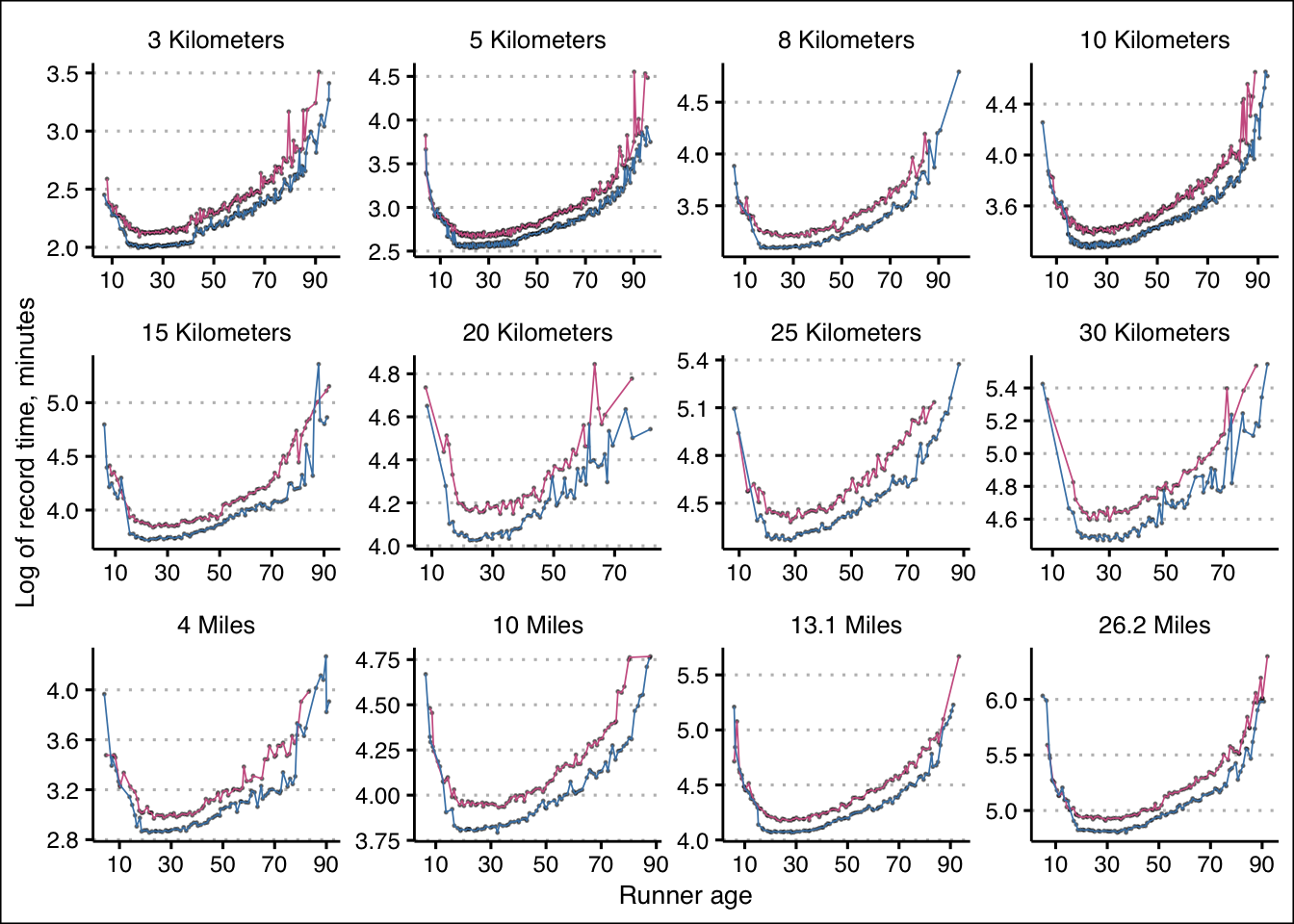
Let’s also consider the log of those record run times to consider the rates of change:

Prior work

Fair and Kaplan (2018) focused on the performance of older athletes. They explored the biological limit of human running speeds by modeling record times at several distances as a function of age for those 40 years and older.

The authors compared multiple models: a linear-quadratic model, a non-parametric model, and both using the extreme value distribution. Justifying the linear-quadratic model, they theorized that may make sense as information suggested that for ages between around 40 and 70, the log of run times increase linearly with age (a constant rate of decline) and in later years, that rate of decline increases. The authors impose a few restrictions on this linear-quadratic model.

Analysis

Of note, a review of Figure ?? above suggests that a linear model doesn’t quite fit what the data suggest (the rate of change does not quite appear to be constant even early on). Regardless, we’ll begin with a model similar to the linear-quadratic model described in Fair and Kaplan (2018).

We’ll use Stan for modeling estimates. For an initial analysis, let’s focus on 5K run times for male athletes aged 40 and over. For our linear-quadratic model, let’s remove from the data what Fair and Kaplan (2018) call “soft observations”; i.e., observed records at a given age that is slower than any record by an older runner:

data {
  int<lower=0> N;
  vector<lower=0>[N] rk_log;
  array[N] int<lower=0> k;
}

parameters {
  real beta;
  real<lower=0> alpha;
  real<lower=0> delta;
  real<offset=70, multiplier=10> k_star;
  real<lower=0> sigma;
}

model {
  beta   ~ std_normal();
  alpha  ~ exponential(1);
  delta  ~ exponential(1);
  sigma  ~ exponential(1);
  k_star ~ normal(70, 10);
  
  vector[N] mu;
  
  for( i in 1:N) mu[i] = beta + alpha * k[i] + 
  (k[i] > k_star ? delta * (k_star ^ 2 - 2 * k_star * k[i] + k[i] ^ 2) : 0);
  
  rk_log ~ normal(mu, sigma); 
}

generated quantities {
  vector[N] rk_log_hat;
  
  for( i in 1:N) 
    rk_log_hat[i] = normal_rng(
    beta + alpha * k[i] + (k[i] > k_star ? 
      delta * (k_star ^ 2 - 2 * k_star * k[i] + k[i] ^ 2) : 0), sigma);
}

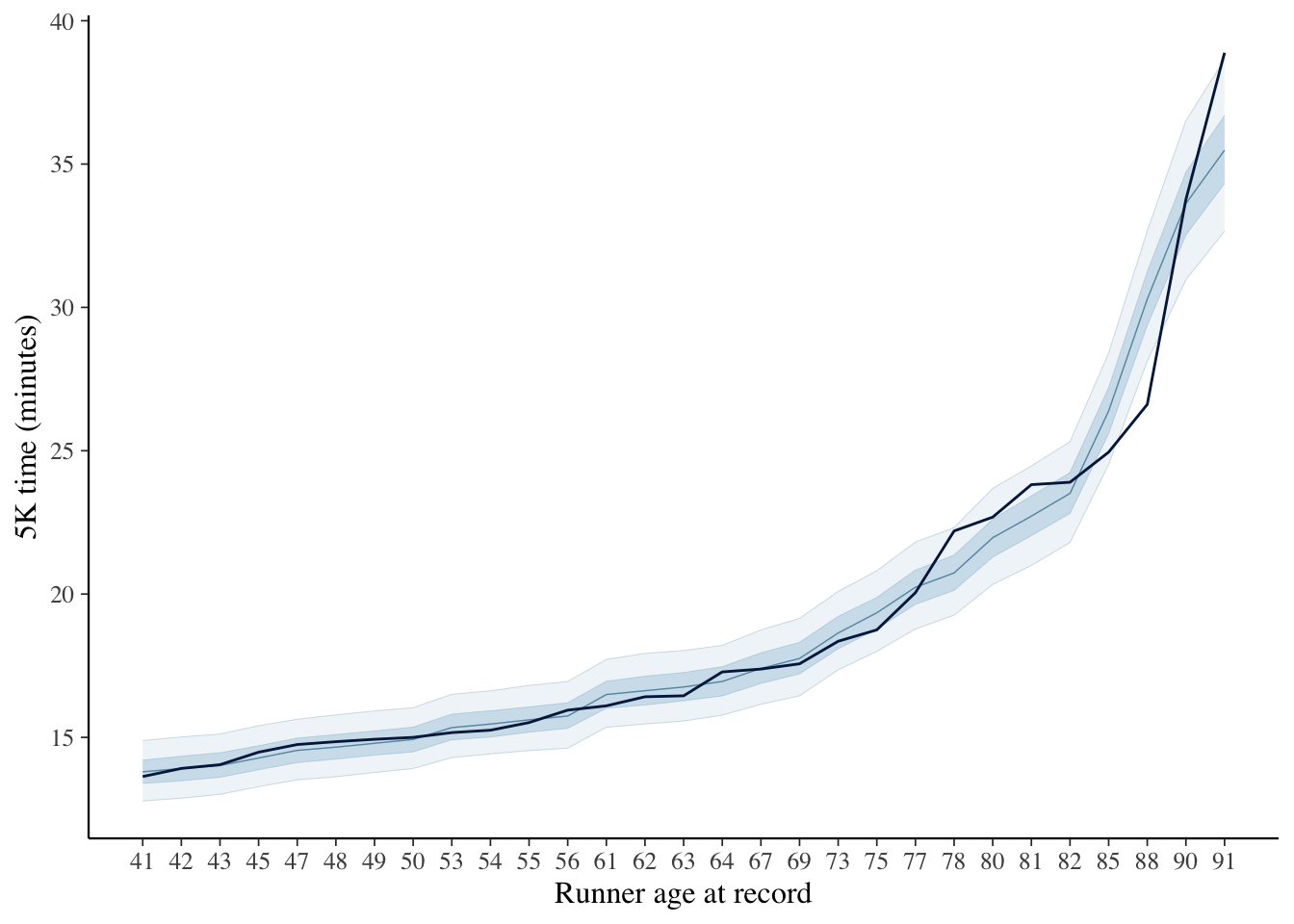
We should probably use more information to set more informative priors. For now, thoug, let’s compare the resulting expectations, conditional on the model and data, with the observed records:

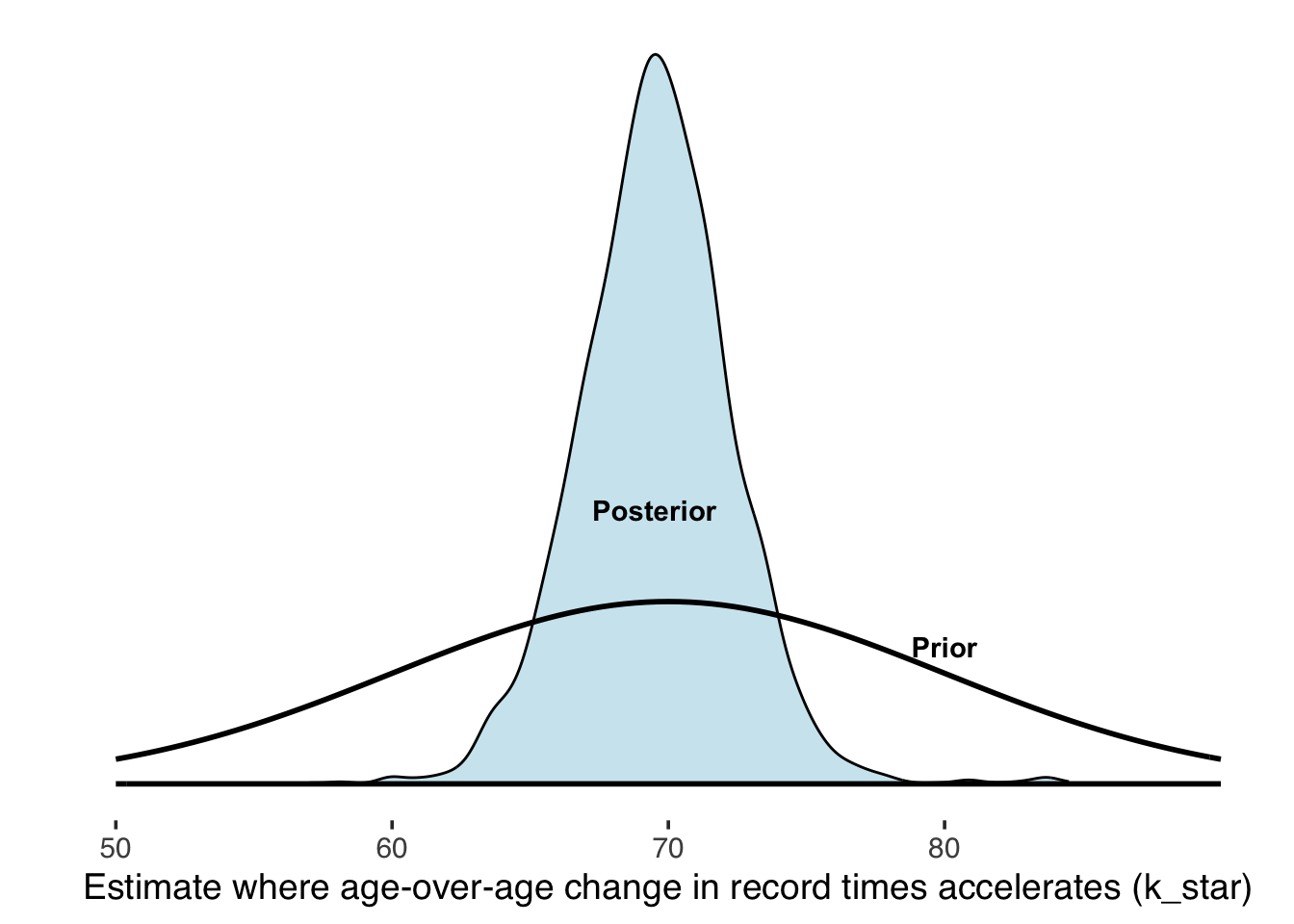
Our posterior estimate for the age where age-over-age change in record times begins to accelerate is around 70, not moving much from our prior’s location, but the data add support by concentrating closer to 70:

Next, let’s consider a nonparametric model based on extreme value theory. Here’s it is, where the biological minimum \(b_k\) is a fraction of the record \(r_k\):

data {
  int<lower=0> N;
  vector<lower=0>[N] rk;
  array[N] int<lower=0> k;
}

parameters {
  vector<lower=0, upper=1>[N] b_;
  real<lower=0> kappa;
  real<lower=0> lambda;
}

transformed parameters {
  vector[N] b = b_ .* rk;
}

model {
  b_ ~ beta(20, 1.5);
  kappa ~ exponential(1);
  lambda ~ exponential(1);
  
  rk - b ~ weibull(kappa, lambda);
}

generated quantities {
  vector[N] rk_hat = 
    rk - to_vector(weibull_rng(rep_vector(kappa, N), rep_vector(lambda, N)));
}

Conditional on this model and data, here are the expectations of the biological envelope, overlain again with the observed records:

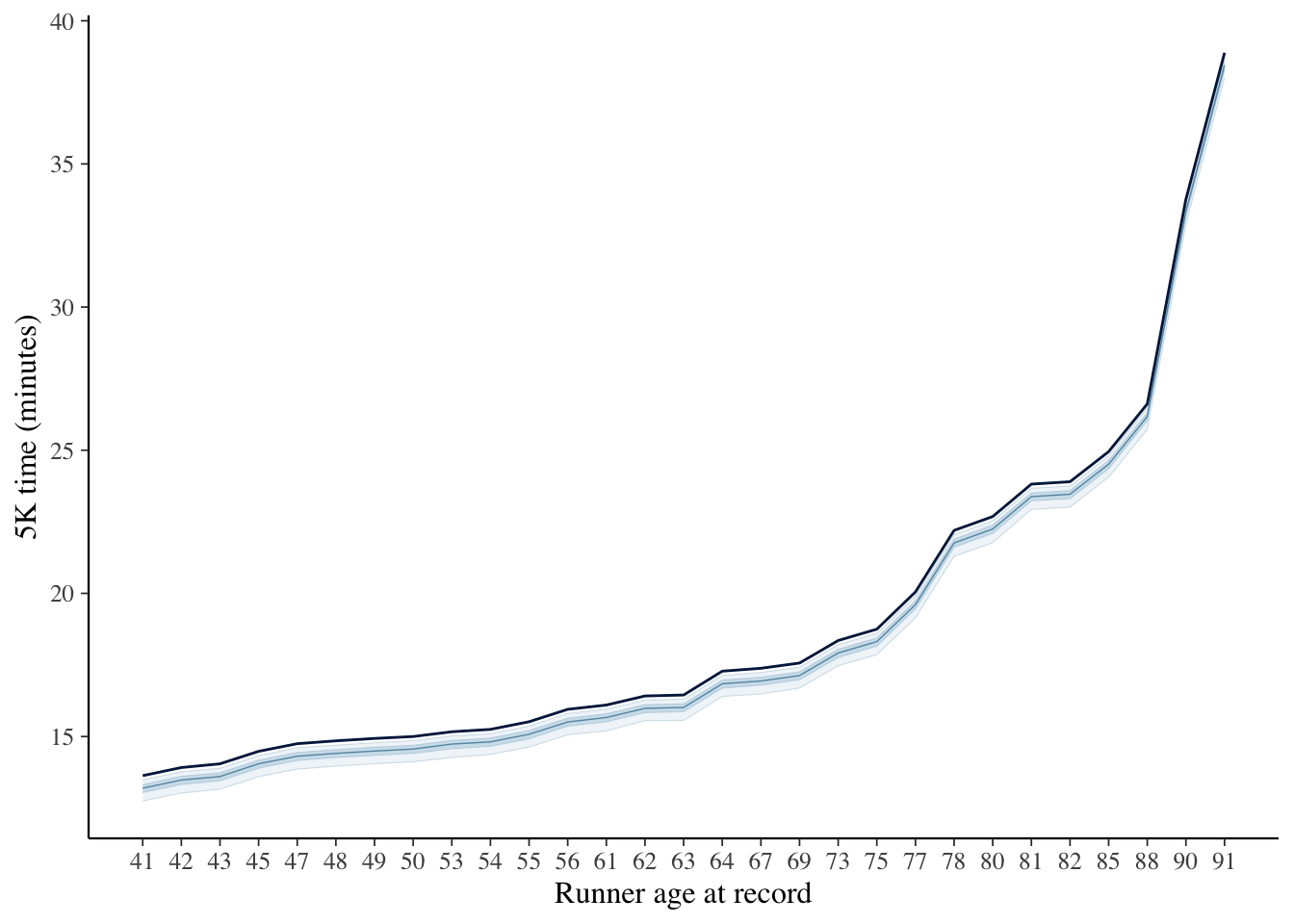
Of note, in this case, I only modeled parameters for ages with data. The estimation of a biological minimum are at and below the trend line of observed records. The estimates, below, of our biological limit \(b_k\) as a fraction of record times are less than 10 percent faster, the uncertainty of which is shown below using the first 200 draws from our model:

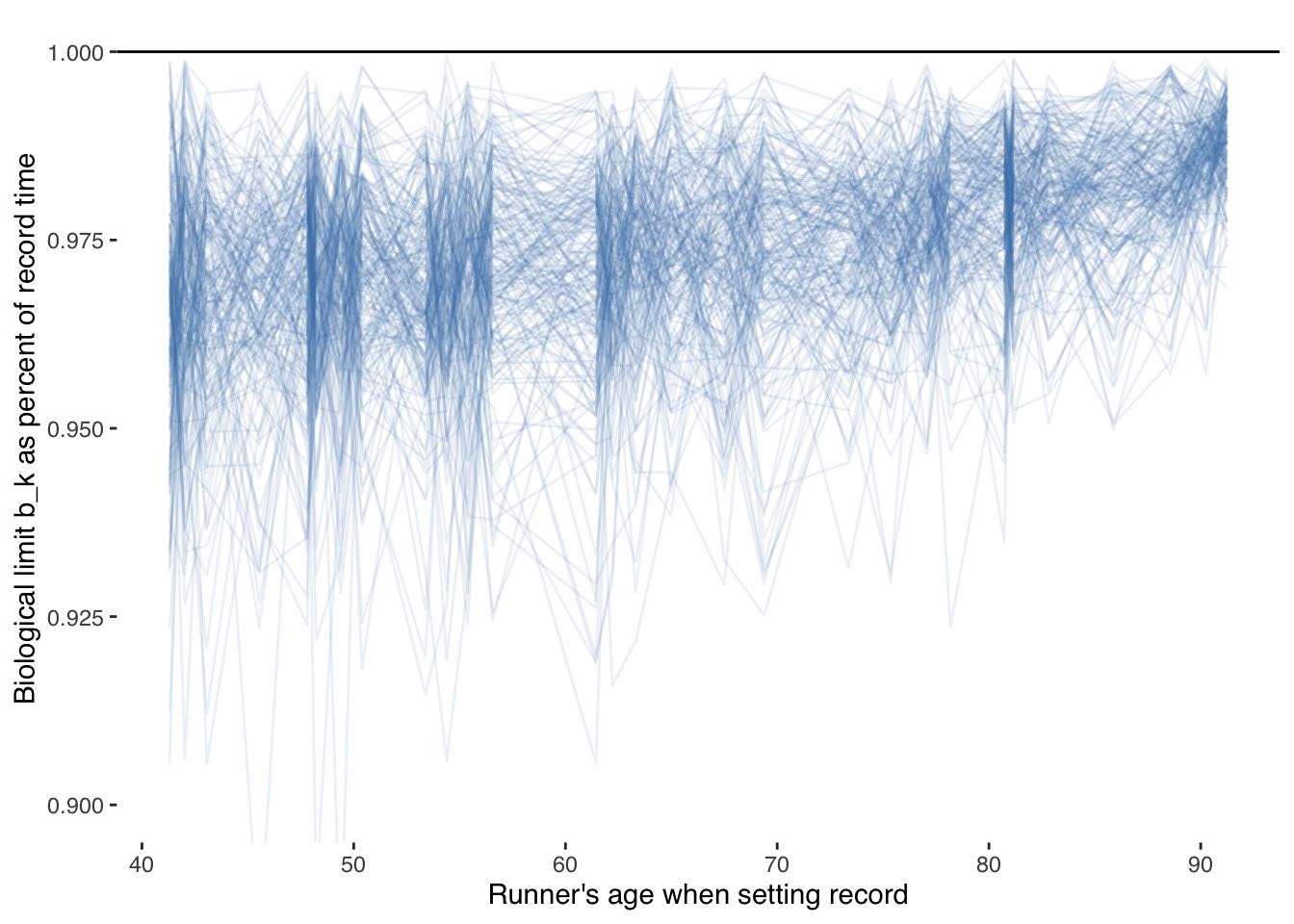
It seems odd that the biological limit would approach the record times as age increases since there are fewer older humans attempting those records.

In a later post, I’ll continue the analysis and, among other things, compare another form of modeling, bring in additional data, and, unlike Fair and Kaplan (2018), account for those “soft observations” instead of simply removing them. With each extension to this analysis, we should learn a little more about what Prefontaine set out to test: the limits of the human heart.